«Математическая составляющая». Главы из книги

Складывание карт

Карты, схемы, путеводители обычно печатаются на больших прямоугольных листах бумаги. Для хранения и переноски эти листы складывают в несколько раз. Самый распространённый тип складывания — прямоугольный: лист разбивается на прямоугольники и складывается по линиям разбиения так, чтобы в сложенном виде у карты не было сгибов большой кратности (как у толстой пачки купюр, согнутой пополам).

При разворачивании карты или схемы проблем нет, но когда вы начинаете складывать карту, часто на каком-то этапе оказывается, что её придётся перегибать в направлении, противоположном тому, что сохранил в своей «памяти» лист.

А можно ли придумать такое разбиение листа карты и такой способ складывания, чтобы:

1. развёрнутая карта складывалась бы «сама» и не было необходимости запоминать порядок складывания;
2. у листа карты в сложенном виде не было сгибов большой кратности.

Сформулированную задачу можно решить, используя приёмы, разработанные японскими мастерами оригами.

Лист карты разбивается на полосы, состоящие из параллелограммов. Если начать складывать такой лист «гармошкой» по вертикали, конструкция автоматически начнёт складываться и по горизонтали. Форма возникшей складчатой поверхности в каждый момент складывания однозначно определяется одним параметром — расстоянием между диагонально противоположными углами карты.

Приведённая конструкция замечательна ещё и тем, что параллелограммы могут быть жёсткими. Это открывает новые возможности для приложений. Например, так устроены солнечные батареи некоторых космических аппаратов.

Цветовые пространства

То, как человек воспринимает цвета, изучали и поэты, и естествоиспытатели, и математики (И. Гёте, Т. Юнг, Дж. Максвелл, Г. Гельмгольц, Г. Грассман и др.). В середине XIX века математик Г. Грассман, один из создателей теории векторных пространств, показал, что цветовое пространство (цветовые ощущения человека) можно рассматривать как «трёхмерное векторное» пространство.

Векторность означает, что вводятся правила сложения цветов и умножения на числа. Сложение — это смешение цветов, умножение на число — изменение интенсивности.

Трёхмерность означает, что, выбрав набор из трёх независимых цветов (т. е. таких, что ни один из них нельзя получить смешением двух других), мы сможем любой различимый глазом цвет получить как их комбинацию. Выбранные три цвета можно воспринимать как базис в цветовом пространстве, а любой цвет — как линейную комбинацию базисных векторов.

Например, из законов смешения цветов, установленных Грассманом, вытекает следующее. Пусть {A, B, C} — некоторый базис в цветовом пространстве, тогда «колоритная» операция смешения цветов с координатами (a₁; b₁; c₁) и (a₂; b₂; c₂) сводится к сложению векторов — итоговый результат будет представлен вектором (a₁ + a₂; b₁ + b₂; c₁ + c₂).

Рассмотрим некоторые употребительные модели цветового пространства.

В мире компьютерных и планшетных экранов — излучающих устройств, свет от которых попадает на сетчатку глаза, — для моделирования восприятия цветов человеком обычно используется модель RGB, предложенная в XIX веке физиком Дж. Максвеллом. В этой модели в качестве трёх базисных цветов выбраны: красный (Red), зелёный (Green) и синий (Blue). Эти цвета независимы — ни один из них нельзя получить как комбинацию двух других.

С другой стороны, большую часть различимых глазом цветов можно получить как их комбинацию. Таким образом, набор R, G, B можно воспринимать как базис в соответствующем «цветовом» трёхмерном пространстве, которое удобно представлять в виде единичного куба. В этой модели координатные оси — базовые цвета R, G, B; начало координат совпадает с вершиной куба и символизирует чёрный цвет («отключены» все цвета, r = g = b = 0). А противоположная вершина куба — «белая» (смешаны все три базисных цвета максимальной интенсивности, r = g = b = 1).

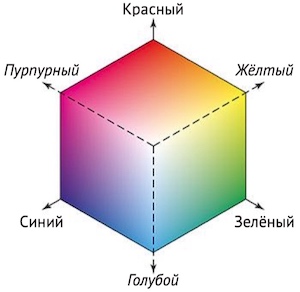
В цветной полиграфии, в том числе и при печати данной книги, основой является другой набор базисных цветов, CMY: голубой (Cyan), пурпурный (Magenta) и жёлтый (Yellow). В единичном «цветовом» кубе система координат, связанная с моделью CMY, следующая: начало координат — вершина куба, представляющая белый цвет, а координатные оси — базовые цвета C, M, Y.

Системы координат базисов RGB и CMY как бы смотрят друг на друга.

То, что в двух приведённых ситуациях (экраны и книги) используются разные модели цветового пространства, довольно естественно. Для экрана компьютера начальное (нулевое, невозмущённое) состояние характеризуется чёрным цветом. Соответственно, начало координат модели RGB — чёрный угол «цветового» куба. Для книги, бумаги первичное (начальное) состояние задаётся белым цветом (никакие краски на лист ещё не нанесены). Соответственно, начало координат модели CMY — белый угол куба.

Взаимное расположение осей, представляющих разные модели (RGB и CMY), определяется физическими соображениями и механизмом возникновения цветовых ощущений у человека. Так, при падении света окрашенный лист бумаги поглощает некоторые цвета, и в отражённом свете мы видим цвета, дополнительные к нанесённым на лист. Получается, что лист воспринимается зелёным, если он окрашен в цвета, дополнительные к зелёному.

Определение дополнительных цветов, которые надо наносить на бумагу, можно провести с помощью простых формул, связывающих координаты цвета (т. е. точки цветового куба) в системах RGB и CMY: цвета (r; g; b) и (c; m; y) совпадают, если

c = 1 − r,
m = 1  − g,
y = 1 − b.

Эти формулы дают ответ на вопрос: как подобрать краску (c; m; y), чтобы залитая ею область воспринималась как область цвета (r; g; b).

Например, чтобы область листа казалось красной, (r; g; b) = (1; 0; 0), её надо залить краской , т. е. смешать краски M и Y, не добавляя С.

Разумеется, приведённые формулы можно читать и «справа налево»:

r = 1 − c,
g = 1 − m,
b = 1 − y.

В этих формулах описано цветовое впечатление, которое сложится, если закрасить область краской (c; m; y).

Для получения чёрного цвета в модели CMY надо смешать три базисные краски максимальной интенсивности: (c; m; y) = (1; 1; 1). Однако полиграфически результат такой операции не очень хорош: есть технологические проблемы, да и при печати текста видно, говоря словами Ильфа и Петрова, что получается не «радикально чёрный цвет». Поэтому к базису добавляют ещё один цвет (обозначаемый буквой K), обычно чёрный, предназначенный, в первую очередь, для печати текста. Такая модель называется CMYK. (И в этой статье в дальнейшем примем за K чёрный цвет.)

При четырёх компонентах CMYK теряется однозначность представления цветов. Например, и доля чёрного (0; 0; 0; 0,2), и смешение трёх компонент (0,2; 0,2; 0,2; 0) соответствуют одному и тому же серому цвету.

Типографские машины наносят краску мелкими точками, которые на каждой (по компонентам CMYK) печатной форме распределяются с переменной плотностью (сами краски по интенсивности одинаковые), что и приводит к меняющейся от области к области интенсивности цвета. Заметим, что при такой технике печати возникает проблема муара — «незапланированного» геометрического узора, возникающего из-за регулярности, правильности решёток. Применяемое на практике решение этой проблемы — чисто геометрическое: муар будет не так заметен, если решётки форм повёрнуты относительно друг друга.

Для выделенной области у каждой печатной формы — своя цифровая инструкция, число от 0 до 1: 0 означает, что в область точки данного базисного цвета ставить не надо, 1 — точки ставятся с максимальной плотностью (полная заливка), а промежуточные значения от 0 до 1 определяют плотность равномерного распределения окрашенных точек в области (отношение площади закрашенной части области к полной). Например, лист розового цвета (как оттенка красного) закрашен редко расставленными точками красок M и Y.

Подчеркнём, что координаты цвета в указанных базисах дают возможность называть цвета не ограниченным набором слов, а точно, наборами чисел. По координатам можно вычислить и ещё одну важную для восприятия цвета характеристику — светлоту. Светлота показывает, насколько цвет «разбавлен белым», «близок» к нему. Базисные цвета модели RGB человек ощущает как цвета различной светлоты. Если принять светлоту чёрного за 0, а белого — за 1, то эмпирически установлено, что в базисе RGB светлота цвета (1; 0; 0) равна 0,299, цвета (0; 1; 0) — 0,587, цвета (0; 0; 1) — 0,114. Векторность цветового пространства — возможность умножать на числа и складывать — позволяет записать формулу для светлоты цвета (r; g; b), «арифметически» описывающую человеческие ощущения:

L = 0,299r + 0,587g + 0,114b.

Заметим, что значения числовых коэффициентов в этой формуле согласуются с тем, что три базисных цвета максимальной интенсивности r = g = b = 1 дают белый цвет.

В цветовом кубе уравнение L = const задаёт плоскость, все точки которой, при выполнении стандартной для графического редактора операции перевода в серую шкалу (Grayscale), переходят в одну точку — точку пересечения этой плоскости с диагональю «чёрный — белый». Таким образом, цветовой куб расслаивается на плоскости одинаковой светлоты.

Базисные цвета модели CMY человеком также воспринимаются как цвета различной светлоты (на рисунке представлены вертикальными полосками). Формулы, связывающие координаты цвета в базисах RGB и CMY, дают аналогичную формулу для светлоты при разложении по второму базису.

Светлоту читатель может представлять как величину, обратно пропорциональную количеству тонера, расходуемого чёрно-белым копировальным устройством при передаче некоторой площади данного цвета. На рисунке левая вертикальная полоса в системе CMY имеет координаты (0; 0,5; 1), правая — (0,38; 0,5; 0). Значения светлоты L для обеих полос совпадают, и их копии, сделанные на чёрно-белом копире, отличаться не будут.

Модели RGB и CMYK — канонические. Конечно, есть и другие модели, например, у дизайнеров популярны системы, в которых светлота становится одной из базисных координат (Lab, HSB). Ситуацию можно сравнить с описанием объектов трёхмерного пространства — можно использовать декартовы координаты (RGB, CMY), а можно — сферические (Lab, HSB).

Случайные блуждания

Станислав Смирнов

Яркий пример полезного взаимодействия, взаимного обогащения математики и других наук — теория случайных блужданий. Эта теоретическая модель не только нашла применения в разных областях от биологии и физики до экономики, но и «помогла» получить несколько Нобелевских премий.

Одно из первых достижений этой теории — объяснение броуновского движения. В 1827 году шотландский биолог Роберт Браун, новаторски использовавший микроскоп, обнаружил явление беспорядочного движения микроскопических частиц в полостях зёрен пыльцы. Изначально надеявшийся, что он открыл «источник жизни», в результате продолжительных исследований Браун пришёл к иному выводу: природа такого движения (называемого сейчас броуновским) — физическая, а не биологическая.

В последующих экспериментах удалось исключить из списка возможных причин хаотического движения и многие физические явления, например испарение, течение жидкости, свет, внешние вибрации...

К концу XIX века получила распространение гипотеза о том, что наблюдаемое поведение частицы в жидкости вызвано столкновениями с движущимися молекулами и атомами (невидимыми в микроскопы того времени). И это несмотря на то, что многие физики (даже великие) ещё не верили в атомное строение вещества. Интересно, что именно изучение математической модели броуновского движения позволило в начале XX века получить одно из первых подтверждений атомной теории.

В физических экспериментах каждая «встреча» частицы с молекулой приводит к сдвигу частицы в каком-то направлении на какое-то расстояние. В математической модели рассматриваются случайные блуждания точки (сохраним для неё название «частица») на плоскости, а чтобы изучение модели стало более простым, предполагается, что поведение частицы менее хаотично и более предсказуемо: для всех столкновений величина сдвига принимается постоянной; направления сдвига — только по сторонам света: север, юг, восток, запад; за определённый интервал времени происходит фиксированное число соударений.

Таким образом, частица может двигаться только по узлам квадратной решётки, а по времени — достаточно равномерно. Можно показать, однако, что эти упрощения не меняют суть, характер изначального случайного блуждания, т. е. модель достаточно точна.

В фольклорном описании этой модели частица представлена матросом, «отдохнувшим» в баре портового города с квадратной сеткой улиц и возвращающимся на корабль. На каждом перекрёстке матрос присаживается, забывает о направлении движения и продолжает путь по одному из четырёх направлений с равной вероятностью (1/4).

Можно рассматривать разнообразные житейские вопросы, касающиеся путешествия моряка, но имеющие математический смысл и в задаче про частицу: попадёт ли когда-нибудь матрос на свой корабль? вернётся ли он в бар, из которого вышел? сколько в среднем времени займёт путь до корабля? как далеко в среднем матрос уйдёт, сделав \(t\) шагов (длина шага — расстояние между соседними перекрёстками)?

Почему возникает необходимость использовать понятие «в среднем»? Дело в том, что при увеличении числа сделанных шагов количество возможных траекторий движения растёт очень быстро: одношаговых — 4, образующихся при двух шагах — 4² и т. д. В случае миллиона шагов число траекторий равно 4^1000000 — это больше, чем число атомов во Вселенной, но в задачах естествознания такие величины встречаются и с ними надо уметь работать. Среди множества траекторий есть сильно отличающиеся: например, матрос может двигаться только вправо (и за \(t\) шагов удалиться на расстояние \(t\)), а может перемещаться и по сложной траектории, когда направление движения меняется почти на каждом шаге.

Но несмотря на такое различие в поведении траекторий можно изучать, как выглядит траектория «в среднем», так сказать, типичная. Например, удивительным и важным фактом (причём по доказательству несложным) является то, что в среднем через время \(t\) частица оказывается от начальной точки на расстоянии порядка $\sqrt{t}$. (После некоторого раздумия такой результат уже не кажется удивительным, ведь матрос часто возвращается назад и в среднем должен уйти на расстояние меньше чем \(t\).)

Постановка задачи о движении частицы по узлам квадратной решётки содержательная, она находит приложения и при большем числе измерений. Но ответы на сформулированные выше вопросы качественно различаются в зависимости от размерности: например, в одномерном и двумерном случаях «матрос» возвращается в бар, а начиная с размерности три это уже не так.

Вернёмся в начало XX века, к истории о том, как броуновское движение подтвердило атомную теорию. В 1905 году, который часто называют «годом чудес» (на латыни annus mirabilis), у Альберта Эйнштейна вышли и работа по специальной теории относительности, и развивающая теорию броуновского движения статья «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты». Это одна из первых работ по статистической физике — физике, в которой работают со случайностью (см. «Как случается закономерность», стр. 178). В этой теоретической статье, приняв гипотезу о молекулярных причинах броуновского движения, Эйнштейн установил пропорциональность величины среднего смещения частицы и $\sqrt{t}$. В полученной им формуле коэффициент пропорциональности зависит от характеристик жидкости (температура, вязкость), размеров частицы и от числа Авогадро (универсальной физической константы, равной числу молекул в определённом количестве вещества). Эйнштейн пишет, что найденное им соотношение можно применить для определения числа Авогадро, если знать среднее смещение.

Если бы удалось экспериментально оценить среднее смещение, то формула Эйнштейна стала бы источником нового способа определения числа Авогадро, ранее найденного в кинетической теории газов. Совпадение старого и нового значений стало бы подтверждением и молекулярной модели броуновского движения, и всей теории атомного строения вещества.

Эту задачу решил французский физик Жан Батист Перрен, которому в 1908 году удалось в серии экспериментов оценить среднее смещение. Число Авогадро было подтверждено, причём с большой точностью, о чём Перрен написал Эйнштейну восторженное письмо. В 1926 году Перрен получил Нобелевскую премию по физике.

До сих пор в математической модели случайных блужданий действовал ряд предположений: постоянство величины сдвига и частоты соударений. А что будет со случайным блужданием, если столкновения происходят всё чаще, а вызванные ими сдвиги становятся всё меньше? Как говорят в математике, «в пределе» случайных ломаных (траекторий) получится случайная функция. Так как характер природных процессов — дискретный, а изменения на каждом шаге очень малы, то подобные функции встречаются часто. Впервые теорию таких функций построил Норберт Винер, известный во всём мире как «отец кибернетики».

У подобных моделей множество полезных применений. Например, ещё в начале XX века Луи Башелье для изучения рынка акций применял случайные блуждания с малым шагом, предвосхитив подход Винера. То, что случайное блуждание является хорошей моделью изменений цены актива на бирже, — довольно естественно. По каждому активу производится множество независимых операций многочисленными игроками, у каждого из которых и для продажи, и для приобретения свои мотивы и обстоятельства — кто-то покупает, думая о вложении на будущее в образование детей, кто-то продаёт... Как результат — цена становится случайным блужданием.

Конечно, есть какие-то общие факторы, систематически влияющие на цену; например, для некоторых позиций это может быть политическая обстановка или цена на нефть. Этот так называемый снос можно представить наглядно на примере блужданий матроса по «наклонной» плоскости: матрос с равными вероятностями идёт на восток и запад, а на север и юг — с вероятностями 1/4 + δ и 1/4 − δ. Вычитание сноса приводит к изначальной постановке задачи случайного блуждания.

Об эффективности случайных блужданий как модели ценообразования говорит присуждение в 1997 году Нобелевской премии по экономике за разработку модели ценообразования опционов (модель Блэка — Шоулза). До появления этого математического результата предсказание изменения цен обычно осуществлялось на основе сравнительного анализа данной траектории с какими-то похожими, имеющимися в биржевой истории. А в этой модели «предсказания» основаны на случайно-непредсказуемом блуждании цен, в частности — на известном нам результате о среднем смещении в броуновском движении на $\sqrt{t}$ за время \(t\).

Стоит оговориться, что любая математическая модель — упрощение действительности, а потому имеет свою область применимости. Модель случайных блужданий не работает в кризисные периоды, когда оценка сдвига на величину $\sqrt{t}$ перестаёт работать. Хорошая модель для кризисов математиками пока ещё не придумана...

Модель случайных блужданий описывается просто, с её помощью уже исследованы многие важные задачи, но связанных с ней интересных вопросов хватит и на XXI век. Для представления новых задач нам понадобится понятие фрактала — самоподобного и сложно устроенного, изломанного объекта дробной размерности.

Самоподобие — это похожесть целого объекта и любого его куска. Сложность, изломанность в дополнение к самоподобию обнаруживаются и в природе, и в модели случайных блужданий. Например, у береговой линии суши малые участки столь же прихотливо изогнуты, что и большие. Аналогично с броуновским движением: детализированное изображение траектории превращает отрезки на «грубом» рисунке в «лохматые ломаные», похожие на общий первоначальный вид.

Для измерения плоских объектов есть два привычных способа: длина — одномерная мера и площадь — двумерная. Площадь кривой нулевая, а вот длина даже у ограниченной, но изломанной кривой может неограниченно возрастать с ростом точности измерений. Получается, что двумерная площадь не различает кривые, в частности, «не видит» сложность, а одномерная длина со сложностью просто не справляется. Желание определить характеристику линии, учитывающую её изломанность, сложность, можно реализовать, введя дробную размерность.

Делается это так. На плоскую ограниченную кривую накладывается «измерительная» сетка из L×L квадратиков. В процессе измерения размеры квадратиков последовательно уменьшают (соответственно растут значения L) и на каждом шаге вычисляют число квадратиков, пересекающихся с кривой. Дробной размерностью кривой называется такое число a, что при больших значениях L число пересечений хорошо приближается значением L^a.

У гладкой кривой такая размерность равна 1, у области — 2, т. е. это соответственно одномерный и двумерный объекты в привычном смысле. Для кривых увеличение дробной размерности от 1 до 2 означает увеличение сложности. Значение размерности, близкое к 2, означает, что некоторые участки плоскости кажутся сплошь закрашенными данной кривой. В природе встречаются и гладкие объекты, и фракталы, у которых значение размерности действительно дробное. Сам термин «фрактал» отражает разные оттенки: в нём есть и изломанность (латинское fractus), и дробность (английское fraction).

Основатель теории фракталов Бенуа Мандельброт заинтересовался размерностями, связанными с броуновским движением. Отображающая его кривая на детализированных «портретах» имеет так много самопересечений, что некоторые участки выглядят как области положительной площади, а броуновское движение кажется двумерным и действительно является таковым, в силу результата, оценивающего среднее смещение как $\sqrt{t}$. Правда, если удалить такие участки и оставить только границу броуновского движения, то она будет очень похожа на некоторые береговые линии — это заметил и сам Мандельброт (вспомним, что его первая работа по теории фракталов называлась «Какова длина побережья Великобритании»). Присмотревшись внимательнее, Мандельброт заметил, что граница броуновского движения очень напоминает другой фрактал, размерность которого считалась равной 4/3, и высказал гипотезу, что и у броуновской границы размерность 4/3.

Этот другой «природный» фрактал — длинная линейная полимерная молекула, типа ДНК. Она умещается в крохотной клетке, поскольку плотно «упакована». Нобелевский лауреат Пол Флори, изучая реальное расположение макромолекул в растворах (такая информация важна, например, для понимания происходящих химических процессов), предложил использовать модель случайного полимера. С математической точки зрения это случайное блуждание без самопересечений, термин — самоизбегающее блуждание.

На языке путешествия матроса это ограничение означает, что теперь ему запрещается возвращаться к тем перекрёсткам, на которых он уже побывал. Такую задачу сложнее изучать, чем броуновское движение, в частности потому, что её нельзя представить динамически. При случайном блуждании без ограничений матросу не нужно помнить своё прошлое. А в самоизбегающем блуждании матросу надо наносить на карту все пройденные перекрёстки и больше туда не возвращаться. Но даже при наличии такой карты матрос в какой-то момент может обнаружить себя взаперти, например, обойдя по кругу группу кварталов и войдя в её внутреннюю часть. Поэтому чтобы изучать траектории без самопересечений фиксированной длины (рассматривая, например, расположения полимерной молекулы), придётся предварительно все их найти.

Понятно, что среднее удаление от начальной точки в самоизбегающих блужданиях будет больше, чем в случайных блужданиях без ограничений, — сказывается запрет на возвращение. Ожидается, что в траекториях без самопересечений среднее удаление за \(t\) шагов будет равно $t^{\mathrm{3/4}}$ (для сравнения: $\sqrt{t}=t^{\mathrm{1/2}}$ у броуновского движения). Пол Флори предположил нестрогий вывод этой гипотезы, из которой вытекает, что возникающие в модели случайного полимера кривые — фракталы размерности 4/3.

Аргументы Флори основывались на изначально нестрогой теории среднего поля Ландау, и довольно быстро коллеги Флори пришли к выводу, что она вносит две ошибки в вычисления. Строгого доказательства всё ещё нет, но недавние работы Лоулера, Шрамма и Вернера дают надежду, что 4/3 — верный показатель степени, т. е. две ошибки непонятным образом взаимно сокращаются.

Все рассмотренные выше примеры фракталов мотивированы природными явлениями. Следующий пример иллюстрирует необходимость изучения фракталов, связанных и с природой, и с технологической деятельностью человека.

Перколяция (от латинского слова percolatio — ‘фильтрация’, ‘процеживание’) — явление часто встречающееся: от просачивания воды через породу или газов через фильтр противогаза до распространения пожаров, эпидемий и даже информации. Математическое моделирование перколяции — создание модели пористого (дырчатого) вещества.

В середине XX века была предложена следующая общая модель перколяции. В плоской сотовой структуре каждая ячейка может быть заполненной (веществом) или пустой — в последнем случае в неё может попасть вода. Выбор характеристики ячейки определяется случайным образом — бросанием монетки.

Может ли через получившуюся пористую структуру сверху вниз просочиться вода? Если плотность пустот очень мала, то вода не проходит вниз, при возрастании плотности — начинает просачиваться, дальнейший рост плотности приводит к увеличению протечек. Конечно, математики изучают не конкретный пример, а вероятность такого события.

Более правильный вопрос: а каковы пути просачивания в модели перколяции? Оказывается, эти пути — фракталы, в случае шестиугольной решётки размерность фрактала равна 4/3. Например, это означает, что при просачивании через решётку, состоящую из 1000 слоёв, длина среднего пути составит (10³)^4/3 = 10 000 — т. е. путь окажется весьма изломанным и длинным.

Показатель 4/3 как размерность фрактала для пути перколяции и границы броуновского движения — результаты совсем недавние, они получены уже в XXI веке. А вот гипотеза Пола Флори, что размерность фрактала в модели случайного полимера тоже равна 4/3, — до сих пор не доказана, хотя мы стали лучше понимать структуру фракталов этого типа. Хочется надеяться, что доказать гипотезу Флори удастся одному из читателей этой книги!