Решения уравнений тоже могут кристаллизоваться

Обычно физики-теоретики, изучая природные явления, находят математическую интерпретацию физических процессов. Однако на днях американские математики, наоборот, нашли интересную физическую интерпретацию некоторых математических законов.

В свежем препринте D. W. Farmer, M. Yerrington, math-ph/0601007 описывается математическая конструкция из области элементарной математики. Рассмотрим синус и косинус, всем известные периодические функции. Их сумма тоже будет периодической. Возьмем теперь сумму большого числа синусов и косинусов с самыми разнообразными периодами и случайными амплитудами. В результате получится практически хаотическая, почти что случайная функция.

Рассмотрим точки, в которых эта функция равна нулю, то есть все решения уравнения «эта функция = 0». Интуитивно понятно, что расположение этих точек на оси тоже будет более или менее хаотическим.

Теперь сделаем некоторое линейное преобразование функции (какое именно — не важно). Получившаяся в результате другая функция будет обладать своим набором решений, а значит, своим набором точек на прямой. Если теперь то же самое преобразование применять многократно, то раз за разом мы будем получать разные наборы точек. Можно сказать, что эти точки «пляшут на прямой» под действием нашего преобразования. Используя физическую аналогию, можно даже говорить о газе точек, которые хаотично скачут по прямой в результате последовательных действий преобразования.

Сумма разнообразных синусов и косинусов (вверху) и результат однократного, трехкратного и десятикратного применения дифференцирования. Положения точек пересечения с осью становятся регулярными (изображение с сайта arxiv.org)

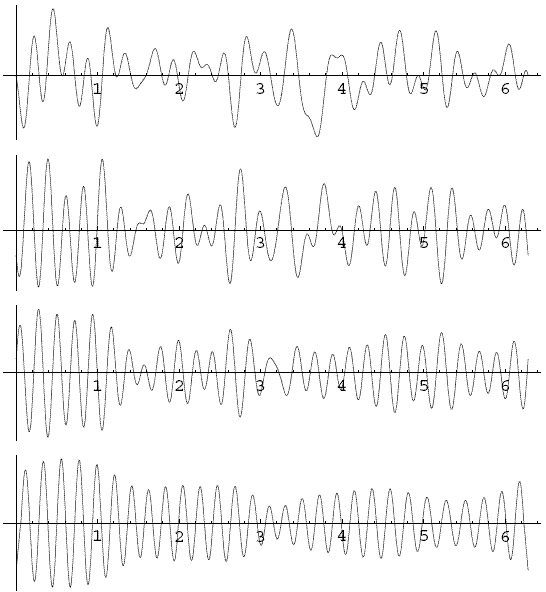
Однако, как выяснили американские математики, эта пляска недолго остается хаотичной. Если в качестве преобразования применять дифференцирование, то можно заметить, что раз за разом прыжки становятся всё меньше и меньше, а относительное расположение точек становится всё более упорядоченным. Спустя некоторое время от некогда бешеной пляски остается лишь мелкое дрожание точек около узлов идеально правильной решетки (см. рисунок). Именно это явления авторы назвали кристаллизацией решений уравнения.

В принципе, с точки зрения математики ничего особо удивительного тут нет. Известно, что после многократного дифференцирования «выживает» функция с минимальным периодом, которая и будет задавать периодичность получающегося кристалла. Интересно, однако, то, что американцам, во-первых, удалось описать происходящие явления именно в физических терминах, а во-вторых, подробно изучить асимптотический закон затухания скачков и «замораживания» решений уравнения. Не исключено, что эти результаты окажутся полезными как для физики, так и в математике, в теории тригонометрических многочленов.

Игорь Иванов