Волны-убийцы: мифы и реальность

Алексей Слюняев, Ефим Пелиновский
«Природа» №10, 2021

Приведен обзор исследований опасного природного явления — неожиданного возникновения необычайно высоких волн на морской поверхности (так называемых волн-убийц). Объясняется, чем такие волны отличаются от обычных гравитационных волн, возникающих под действием ветра, и какова, согласно базовым теоретическим моделям, вероятность образования высоких волн. В простой форме приводятся основные предположения, которые заложены в существующие модели прогноза ветрового волнения, и показано, в чем их недостаточность для объяснения появления волн-убийц. Обсуждается связь волн-убийц с ключевыми решениями приближенных уравнений гидродинамики (солитонами, солитонами огибающей, бризерами), а также неоднозначный взгляд на роль эффектов нелинейной самомодуляции волн в открытом океане. Приводится общая гипотетическая концепция прогноза ветровых волн в океане и обсуждаются новые подходы для прогноза волн, учитывающие эффект волн-убийц.

Об авторах

Алексей Викторович Слюняев — доктор физико-математических наук, профессор РАН, заведующий сектором моделирования экстремальных волновых явлений в океане Института прикладной физики РАН, профессор НИУ ВШЭ. Область научных интересов — нелинейные морские волны, нелинейные эволюционные уравнения. Лауреат медали РАН с премией для молодых ученых (2006) и премии имени Л. И. Мандельштама РАН (2018).

Ефим Наумович Пелиновский — доктор физико-математических наук, профессор, главный научный сотрудник того же института, профессор Нижегородского государственного технического университета и НИУ ВШЭ. Лауреат Государственной премии России (1997) и премии имени Л. И. Мандельштама РАН (2018). Занимается разработкой физико-математических моделей волновых процессов и их применением в прогнозировании морских природных катастроф.

Наша статья мотивирована тем, что вокруг темы морских «волн-убийц» возникло множество кривотолков. Проблема высоких волн, неожиданно появляющихся на поверхности океана, перешла в плоскость научной относительно недавно: в конце 1990-х годов — начале 2000-х. Таким образом, ее «научный» возраст примерно лет 20, и сейчас она продолжает привлекать огромное внимание как исследователей, так и общественности. Хотя предстоит еще многое понять и сделать, достигнут некоторый переломный момент, когда в большой степени уже стало ясно, с какими физическими явлениями связаны волны-убийцы и в каком направлении нужно двигаться дальше¹.

На удивление, до сих пор нет единого общепринятого определения, что же понимается под волнами-убийцами. Подобное определение с физической точки зрения мы попытались сформулировать в «Большой российской энциклопедии», его и придерживаемся в этой статье. Абсолютное большинство существующих определений базируется на амплитудном критерии: это волны, которые выше обычных во столько-то раз. Для человека, плывущего на корабле, наиболее естественной характеристикой размера волны кажется ее высота от ложбины до гребня. Для наблюдателя на стационарной платформе (например, установленной на морском шельфе для добычи нефти и газа) наиболее существенна самая верхняя часть волны и высота ее гребня относительно невозмущенного состояния. Добавим еще, что сами высоты можно измерять разными способами, а в определении волны-убийцы учитывать дополнительные факторы, важные для конкретных приложений (асимметрия формы, обрушение и др.) [1]. Отсутствие однозначного определения и «горячность» темы объясняют будоражащие воображение выдумки. В то же время существует немало объективных обстоятельств, которые препятствуют созданию ясного портрета явления и скорому раскрытию практически важных загадок, связанных с аномальными морскими волнами.

Волны-убийцы, цунами, солитоны...

Определим четче предмет нашего разговора. В общем смысле под волнами-убийцами подразумевают необычайно интенсивные волны, которые возникают неожиданно. Их еще часто называют аномально высокими, просто аномальными или экстремальными, хотя в таком случае очевидно расширение понятия: не всякая большая волна неожиданная. В отечественной прессе можно встретить названия блуждающие волны или волны-шатуны, хотя нам истоки их происхождения не вполне понятны. Вполне возможно, что они идут от другого очень интересного класса волн — солитонов, которые способны пробегать без изменения весьма большие дистанции².

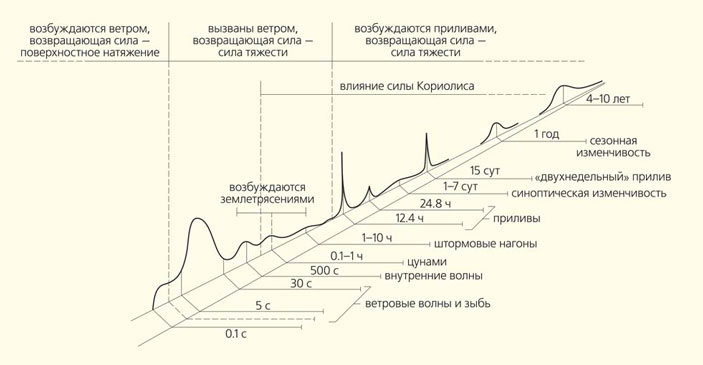
Под морскими волнами-убийцами понимаются очень большие волны, неожиданно возникающие в поле нерегулярных волн, которые создаются на поверхности ветром (ветровые волны). Потому другое широко известное океанское катастрофическое явление — волны цунами — не имеет прямого отношения к волнам-убийцам. Они отличаются, во-первых, масштабом: ветровые волны много короче (от сотни до нескольких сотен метров, периодом от нескольких до 10–15 с). На рис. 1 приведено распределение энергии волновых движений в океане по периодам в глобальном масштабе. Из него следует, что при всей «заурядности» ветровых волн и зыби (т. е. более длинных старых ветровых волн, которые уже не ощущают силы ветра) на них приходится большая доля энергии, превосходящая и цунами, и приливные волны. Кроме того, как было поэтично сформулировано в заголовке одной из исследовательских работ, волны-убийцы «возникают ниоткуда и уходят в никуда» [3]. Кажется, что проследить ранние стадии их зарождения невозможно.

Рис. 1. Распределение энергии волновых движений в Мировом океане по характерным периодам [2]

В англоязычной литературе (представляющей преобладающую часть исследований по этой теме) соотносимые с волнами-убийцами названия многочисленны. Наиболее распространенные на сегодняшний день — rogue waves и freak waves. Современные наблюдения волн-убийц собираются в каталоги и анализируются для вычерчивания общей картины необычных опасных волн [4, 5]. Места их наблюдений в 2011–2018 гг., по сообщениям очевидцев, приведены на рис. 2, а. Из него следует вывод, что такие волны встречаются практически повсеместно. Большая часть наблюдений ожидаемо приходится на береговую зону, где присутствие человека максимально (рис. 2, б).

Рис. 2. Места событий волн-убийц в мире, по данным СМИ в 2011–2018 гг. (а) и распределение случаев по местам их возникновения (б) [4]

Как упоминалось выше, для выделения класса волн-убийц используется амплитудный критерий, который может быть записан в следующем виде:

(1)       \(\frac{H}{H_s} > R\),

где H — высота волны, H_s — некоторая средняя (так называемая значительная) высота волн, а R — константа. В океанографии значительная высота определяется как среднее от трети наибольших высот волн в выборке. Наиболее часто пороговую константу R в определении (1) принимают равной 2 или 2.2.

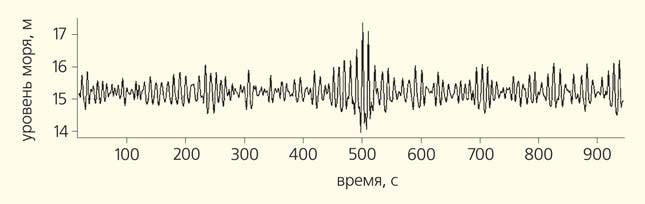
Рис. 3. Запись волнения в районе устья оз. Изменчивого (о. Сахалин), содержащая аномальную волну с усилением H/H_s = 2.65 [6]

Как же мерить высоту волны, если ее гребень расположен в одной точке, ложбина в другой, а вся поверхность постоянно меняется? Измерения морских волн на регулярной основе начались в середине XX в. Их абсолютное большинство представлено записями смещения границы раздела вода—воздух в одной точке, где установлен измеритель (плавающий заякоренный буй, закрепленный на платформе лазерный высотомер, расположенный на дне датчик избыточного давления и др.). Пример такой записи (мареограммы) волны-убийцы у берегов Сахалина дан на рис. 3. Короткие отрезки других мареограмм из Индийского океана, содержащих волны-убийцы разной формы, приведены на рис. 4. Некоторые записи аномальных волн оказались настолько популярными, что получили собственные имена: Новогодняя волна, волны Андреа, Киллард, Юра. В наше время непрерывные измерения волн могут осуществляться месяцами. Чтобы записи соответствовали примерно постоянным (квазистационарным) условиям волнения, длинные последовательности данных разбиваются на интервалы по 10–30 мин. Потому каждая мареограмма содержит пару сотен периодических осцилляций поверхности около состояния равновесия — индивидуальных волн. По получившимся зависимостям смещения поверхности от времени η(t) и определяют высоты волн [2] — как разность между амплитудами пар соседних ложбин и гребней (рис. 5).

Рис. 4. Разные формы волн-убийц, зарегистрированных буем у берегов Индии: а — высокий гребень, б — знакопеременная волна, в — «дырка в море», г — интенсивная группа [7]

Рис. 5. Анализ временной записи смещения поверхности η(t) в соответствии с методом zero down-crossing (по пересечению нулевого уровня вниз). Индивидуальная волна заключена между голубыми точками. Ее высота равна сумме амплитуд гребня A_cr и ложбины A_tr

Раз мы говорим про большие морские волны, то первый вопрос: а насколько высокими они бывают? Процитируем научно-популярную книжку 50-летней давности: «Большинство океанских штормовых волн имеет в высоту 4–4.5 м. Волны выше 6–7 м — довольно редкое явление. Что же касается максимальной высоты волн, то в различных областях океана она может быть разной, но, в общем, не превышает 20 м» [8]. По данным инструментальных измерений, выполненных уже в XXI в., 30-метровые волны регистрировались неоднократно. Отметим, что в масштабе Мирового океана более высокие волны возникают вдали от берегов, в акваториях большой площади (на них ветер успевает вырастить гигантские волны), где раньше судоходные пути не прокладывались. С ростом интенсивности трансокеанских перевозок шанс встретить такого водяного монстра тоже растет.

Такие частые редкие волны

Оценка вероятности возникновения волн с заданной высотой — ключевая характеристика в инженерии. Она требуется для определения норм строительства и использования судов и сооружений, которые должны быть достаточно безопасны в течение срока своей эксплуатации. Слишком частый ремонт кораблей и океанических платформ и выплата страховок могут оказаться чрезмерно дорогими. С другой стороны, создание избыточно безопасных сооружений — еще дороже. С точки зрения страховых выплат критическим служит разделение на нормальные события (которые укладываются в рамки оценок их вероятности, использованных страхующей компанией) и форс-мажорные. Гибель матроса на советском танкере «Таганрогский залив» от внезапно появившейся волны повлекла судебное разбирательство с привлечением научной экспертизы [9, 10]. В расследованиях разлома танкера «Prestige» пополам и его затопления³ в 2002 г. (рис. 6) и гибели двух пассажиров на лайнере «Louis Majesty» в 2010 г. также привлекались экспертные мнения специалистов по волнам-убийцам.

Рис. 6. Авария танкера «Prestige»

Для применения в судостроении можно определять максимально возможные волновые нагрузки, реализуемые один раз в течение срока эксплуатации корабля (например, 25 лет). Два временных интервала прописаны в нормах норвежской стандартизирующей компании «Det Norske Veritas», они используются для нефтегазодобывающих платформ. Один раз в 100 лет волна может захлестнуть надстройку платформы, но это не должно привести к существенным разрушениям или травмам персонала. Не чаще, чем раз в 10 тыс. лет, может произойти повреждение оборудования платформы, но при этом не допускается ни полного разрушения сооружения, ни существенного экологического загрязнения, а персонал должен иметь возможность эвакуироваться. Таким образом, для оценки рисков, связанных с возникновением экстремальных волн, требуется аккуратно учитывать очень редкие события их появления.

В первом приближении теория ветровых поверхностных волн рассматривает возвышение свободной поверхности как бесконечную совокупность простых гармонических волн с разными длинами и амплитудами, бегущих в определенных направлениях (рис. 7) и никаким образом не связанных между собой. Тогда, согласно хорошо известной центральной предельной теореме, движение поверхности представляет собой случайный стационарный гауссов (нормальный) процесс. При дополнительном условии узости спектра волнения (длины наиболее интенсивных волновых компонент не сильно отличаются) вероятность P превышения заданной высоты H описывается распределением Рэлея:

(2)       \( P(H) = \exp\left(-\tfrac{H^2}{8\sigma^2}\right) \approx \exp\left(-2\tfrac{H^2}{H_s^2}\right) \),

где σ — среднеквадратичное смещение поверхности. Распределение (2) получается на уровне теоремы теории вероятностей, и отклонения от него возможны лишь при нарушении заложенных в модель предположений. Связь между среднеквадратичным отклонением σ и значительной высотой H_s ≈ 4σ следует непосредственно из соотношения (2).

Рис. 7. Морская поверхность как суперпозиция синусоидальных гармоник

Распределение Рэлея (2) может быть легко использовано для оценки вероятности появления волн-убийц. В частности, при выборе в определении (1) пороговой константы R = 2 получаем вероятность P(H/H_s = 2) ≈ 0.00034, что означает: в среднем одна волна из примерно 3 тыс. будет вдвое выше H_s и потому ее можно назвать волной-убийцей. Для R = 2.2 вероятность P(H/H_s = 2.2) ≈ 0.000063, и здесь волной-убийцей может быть названа уже лишь одна из 16 тыс. волн. Если далее в качестве оценки периода волн выбрать 10 с, то в первом случае одна волна-убийца возникает примерно каждые 8 ч, во втором же — раз в двое суток, а для R = 3 — один раз более чем в 20 лет. Таким образом, использование в определении (1) порога R = 2 задает волну-убийцу как максимальную волну за типичное время шторма в 6–8 ч, что делает выбор такого определения волны-убийцы осмысленным.

Насколько реалистичны сделанные выше оценки вероятности образования волн-убийц? Если каждые 8–9 ч регистрируется волна-убийца, то в сутки получается уже три таких волны. Это, на первый взгляд, не вяжется с ожидаемой исключительностью подобных экстремальных волн. Если раньше из-за технических ограничений измерения волн проводились эпизодически (например, буй «просыпался» каждый час на 10 мин, регистрировал волнение и сохранял в долговременной памяти только его усредненные характеристики), то сейчас накоплены данные измерений, насчитывающие миллиарды индивидуальных волн. В чем же подвох? Во-первых, с практической точки зрения важна высота по абсолютной величине, что не учитывается определением (1). Волны с высотами менее 1 м часто не считаются опасными в принципе. Во-вторых, требуется очень много данных. Временной ряд в 10 тыс. лет содержит около 30 млрд волн. Если верить распределению (2), то одна из них сможет достигнуть усиления в 3.5 раза. Чтобы провести статистическое осреднение, подобные события должны быть измерены неоднократно. Имеющиеся данные измерений, хоть и кажутся огромными по объему, не позволяют дать определенных ответов даже относительно вероятности намного более частых (и менее экстремальных) событий.

Например, на основе обработки записей 1.1 млрд индивидуальных волн, сделанных вдоль берегов Америки [11], было выделено 75 тыс. волн-убийц с превышением высоты H/H_s > 2, включая 120 волн с усилением H/H_s в интервале от 3 до 4; 30 волн с усилением в интервале от 4 до 5 и 19 волн с H/H_s > 5. Легко прикинуть, что в среднем одна волна-убийца приходится на 15 тыс. волн — в пять раз реже, чем следует из распределения (2). С другой стороны, согласно рэлеевской статистике (2), усиление H/H_s = 5 для волн с периодом 10 с должно соответствовать повторяемости событий один раз в 10¹⁵ лет, что на пять порядков превышает возраст Вселенной. Накопленные измерения демонстрируют сильную географическую и сезонную изменчивость вероятности возникновения волн-убийц, т. е. они статистически неоднородны. Можно предположить, что и физические механизмы появления волн-убийц в разных местах различные. Очевидно также, что для постоянно изменяющихся условий моря измерения, выполненные в одной и той же точке в разное время, могут соответствовать процессам с различным распределением вероятностей, поэтому они должны обрабатываться отдельно.

Проблема качества измерений добавляет неопределенности. В исследовании М. Кристу и К. Эванса (122 млн волн, записанных разными устройствами) особое внимание уделялось многоступенчатому контролю качества данных [12]. В результате было отсеяно 18% мареограмм, не содержащих аномально высоких волн, и 84% (!) записей с волнами-убийцами. Таким образом, хотя было обработано более 3.5 тыс. аномальных волн, полученная статистика могла стать заложницей неоднородного контроля качества (что признавалось и самими авторами работы). Известны и другие примеры ошибочных измерений (например, из-за инерции буев, нечеткости границы вода—воздух при наличии сильных брызг или дождя, из-за отражения волн от опор платформы, на которой установлен измеритель, и др.). В другом примере исследования записей волн с платформы в Индийском океане в течение шести лет одна из зарегистрированных волн обладала высотой 71 м, а четыре — 40–50 м [13]. При этом технические характеристики прибора позволяли измерить лишь 43-метровую волну, а глубина места составляла всего 100 м. При очевидной ошибочности некоторых записей авторы работы не смогли их отбраковать по каким-либо формальным признакам.

Рис. 8. Усредненный профиль волн-убийц (черная линия) и 1% «нормальных» волн с максимальной амплитудой гребня (красная линия), по результатам обработки натурных измерений [12]

На основе большого количества измеренных экстремальных волн можно дать условный портрет наиболее типичной волны-убийцы. Несмотря на разнообразие форм подобных волн, измеренных в различных местах в разное время (см. рис. 4), исследователи вполне сходятся в описании характерной волны: наиболее часто это единичный высокий гребень в составе короткой группы, заключенный между более мелкими ложбинами. На рис. 8 такой профиль построен в нормированных координатах в сопоставлении со средним профилем одного процента наиболее высоких волн, которые не выполнили критерий H/H_s > 2. Если верить приведенному «портрету», аномальные волны довольно похожи на нормальные, только они выше и к тому же сильнее локализованы. В ряде исследований были обнаружены исключительные особенности волн-убийц: асимметрия профиля, аномально долгое существование. Но они пока не вполне подтверждены.

Таким образом, несмотря на технический прогресс и внушительный массив накопленных измерений, натурные данные пока не способны уверенно ответить даже на простой вопрос: возникают ли волны-убийцы чаще, чем предсказывает распределение Рэлея (2), или реже. Результаты разных исследований анализа натурных данных приводят к противоположным выводам. Отметим, что в области высот H < 2H_s распределение (2) довольно хорошо описывает экспериментальные данные, а в ряде хорошо контролируемых численных и лабораторных экспериментов регистрировалась значительно большая доля волн с высотами H > 2H_s, чем это предсказывалось теоретической кривой. Мы предполагаем, что неоднозначный результат исследования натурных данных может быть связан с излишне общей постановкой вопроса. В действительности же в зависимости от ситуации могут реализовываться и нормальные условия (когда распределение (2) работает), и аномальные. Тогда ключевым становится вопрос о физическом механизме, который обеспечивает такой аномальный режим волнения, и об условиях его включения.

Простые формулы для сложной динамики

По поверхности океана в нерегулярных волнах распределена энергия. Она связана с периодическими возвышениями и проседаниями поверхности, которые сочетаются с движением водных масс. Неожиданно высокая волна может сформироваться в каком-то месте в случае быстрой передачи ей большой порции энергии, что подразумевает очень мощное воздействие, на которое ветер не способен. Более реалистичным видится сценарий, когда часть энергии волн с какого-то относительно большого участка поверхности моря собирается на меньшей площади — фокусируется.

Для описания волновых процессов удобно представление в виде интегралов или рядов Фурье, практически повторяющих классические предположения об устройстве волн на воде. Для простоты рассмотрим плоскую задачу, предполагая, что все волны бегут вдоль одной выбранной оси Ox, и будем считать, что смещение поверхности η(x, t) как функция координаты и времени представимо в виде ряда:

(3)       \(\eta = \sum\limits_{k} a_{k} \cos\left(\omega_{k} t — k x + \varphi_{k}\right)\),

где a_k и φ_k — соответственно амплитуды и фазы гармоник, пронумерованных волновым числом k > 0, а зависимость циклической частоты ω_k = ω(k) описывает так называемую дисперсию волн. Без ограничения общности можно считать амплитуды a_k неотрицательными величинами, а фазы φ_k выбирать в интервале от нуля до 2π. Спектр волн S задается распределением амплитуд гармоник a_k по волновым числам. Если фазы φ_k выбираются случайным образом, то решение (3) описывает случайные волны с заданным спектром. Именно спектры волнения служат выходными данными всех численных моделей, которые используются в наше время для прогноза ветрового волнения в океане. Зависимость, представленная на рис. 1, также может быть отнесена к спектрам, только по оси там отложены периоды волн.

Ряд (3) описывает сложную картину суперпозиции гармоник в различных точках в разные моменты времени. При удачном стечении обстоятельств (т. е. подборе фаз косинусов) амплитуды гармоник суммируются, что приводит к появлению волн большой амплитуды в определенной точке в данный момент времени (пространственно-временная_ фокусировка). Волна с максимально возможной амплитудой A_max получается, когда все гармоники оказываются в фазе:

(4)       \(A_{\max} = \sum\limits_k a_k\).

Если в спектре представлены, скажем, только три волны с волновыми числами k₁, k₂, k₃ и идентичными амплитудами a₁ = a₂ = a₃ = a (а все остальные a_k = 0), то при их сложении амплитуда утроится, т. е. A_max = 3a.

Из сопоставления уравнений (3) и (4) можно видеть, что при выборе параметров фаз равными нулю (φ_k = 0) максимально возможная амплитуда A_max возникает в момент времени t = 0 в точке x = 0. В таком случае временная запись решения в точке x = 0 следует из решения (3) η_max(t) = η(x = 0, t):

(5)       \(\eta_{\max}(t) = \sum\limits_k a_k \cos(\omega_k t)\).

Заметим, что полученный таким образом профиль максимально возможной волны (5) полностью определяется спектром волн (набором a_k для данного множества частот ω_k). Формы спектров морских волн отнюдь не случайны: они определяются особенностями физических механизмов генерации волн ветром и затухания, а также связями между гармониками. Последние эффекты нелинейны и не учитываются в решении (3). Полученный по результатам многолетних измерений в Северном море профиль спектра JONSWAP (Joint North Sea Wave Project) и соответствующая ему максимальная волна представлены на рис. 9.

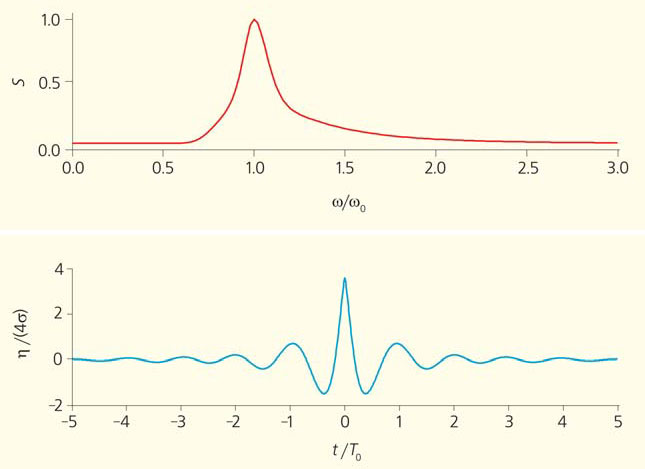
Рис. 9. Форма спектра JONSWAP (вверху) (по вертикали отложен квадрат амплитуды в нормированных единицах, S) и профиль максимально достижимой волны (внизу). ω₀ и T₀ = 2π/ω₀ — циклическая частота и период, соответствующие пику спектра

Несложно показать, что при заданной энергии E волн в бассейне⁴

(6)       \(E = \sum_k a_k^2\)

максимальное значение величины A_max достигается в том случае, когда все a_k равны. Пусть число гармоник, составляющих волновое поле, равно N, а амплитуда каждой из них равна a. Тогда максимально достижимое смещение поверхности в результате суперпозиции всех волн равно

(7)       \(A_{\max}^{\text{(sup)}} = aN = \sqrt{EN}\).

Если при сохранении общей энергии E = a₂N число участвующих гармоник N растет (спектр уширяется), то увеличивается и максимальная высота. В случае бесконечно большого числа гармоник мы приходим к функции η_max(t) с бесконечной амплитудой. Если не все a_k в спектре равны, то значения A_max будут меньше оценки (7) для той же полной энергии (E) волн.

Приведенная здесь математическая иллюстрация способна неплохо описывать эффекты пространственно-временной суперпозиции неоднородных поверхностных волн, которые происходят в реальном море ежесекундно. Можно выделять физические причины, обусловливающие такую фокусировку: дисперсионное сжатие (за счет разных скоростей распространения волн различной длины) или геометрическая фокусировка (схождение разных волновых систем, двигающихся в разных направлениях). Изменение условий распространения (например, переменная глубина, сильные неоднородные течения и др.) также способно приводить к фокусировке энергии поверхностных волн.

N нелинейных волн против девяти линейных В 1960-х годах был обнаружен эффект самомодуляции поверхностных волн [14]. Он заключается в том, что цуг волн примерно одинаковой длины и высоты со временем разбивается на группы, т. е. становится модулированным по амплитуде. Этот эффект кажется неожиданным: раз волны одинаковой длины, то и скорость каждой из них в последовательности должна быть одинаковая. Тогда каким образом в цуге происходит перераспределение энергии? Оказывается, что в условиях глубокой воды волны достаточно большой амплитуды неустойчивы: малые возмущения последовательности волн экспоненциально нарастают во времени. Происходит это вследствие зависимости скорости волны от ее амплитуды (потому и эффект — нелинейный): большие волны бегут чуть быстрее маленьких. Из-за сложной игры эффектов дисперсии и нелинейности волны с чуть большей амплитудой становятся еще выше за счет уменьшения других волн.

Хотя исторически эффект нелинейной самомодуляции впервые был открыт для волн на воде, сегодня мы с ним чаще сталкиваемся в оптических приложениях — как с одним из способов создания очень коротких и мощных лазерных импульсов. В отношении волн в открытом океане до недавнего времени существовало несокрушимое мнение о нереализуемости модуляционной неустойчивости. Действительно, довольно быстро после открытия явления самомодуляции было обнаружено, что этот эффект ослабевает и полностью исчезает, когда цуг волн недостаточно однороден, волны бегут под разными углами или если вода мелкая.

Рис. 10. Схематическое описание процесса модуляционной неустойчивости однородной волны. Красными столбиками показаны амплитуды спектральных компонентов, синими кривыми — зависимость инкремента модуляционной неустойчивости волны, зеленым штрихом — максимальное усиление волн в соответствии с бризерным решением

На спектральном языке однородный цуг волн, описываемый выражением (3), представлен одной единственной гармоникой. Обозначим ее частоту ω₀, а амплитуду, как и ранее, — a. Модуляционная неустойчивость заключается в передаче энергии от этой (основной) гармоники другим, с близкими периодами (и длинами) волн (как показано стрелками на рис. 10). На оси частот (и волновых чисел) получающие энергию гармоники расположены вблизи от основной гармоники, с обеих сторон. В результате этого процесса происходит уширение спектра: энергия из одной гармоники ω₀ переходит в более широкую полосу частот. На примерах в предыдущем разделе мы видели, что когда энергия распределена среди большого числа гармоник, то при подходящем подборе их фаз могут возникать волны с гораздо большей амплитудой. Качественно схожий процесс происходит и в описываемом здесь нелинейном случае: после передачи энергии основной гармоники многим ее соседкам по спектру на короткое время гармоники складываются синфазно и производят большую волну. Чем длиннее растущее возмущение, тем с большего пространства энергия основной волны передается в соседние спектральные гармоники и тем значительнее их усиление.

Рис. 11. Аналитическое решение для огибающей волн — бризер Перегрина (нормированные оси)

Оказывается, что эта динамика описывается точным решением уравнения (хотя и приближенного), которое учитывает эффекты дисперсии и нелинейности в предположении их слабости (нелинейное параболическое уравнение, или нелинейное уравнение Шрёдингера). На рис. 11 такое решение построено в осях координаты и времени, где изображенная поверхность соответствует не границе раздела воды и воздуха, а накрывающей волны поверхности (называемой огибающей) в сопровождающей системе отсчета. Интересно, что в рамках этой приближенной модели процесс модуляционной неустойчивости полностью обратим. После экспоненциального нарастания амплитуд соседних гармоник наступает стадия насыщения. Затем энергия возвращается в основную гармонику (рекурренция Ферми—Паста—Улама). Из-за такой специфической «дышащей» динамики решение называют бризером (breather). В соответствии с ним в предельном случае бесконечно длинного возмущения, собирающего энергию со всего бесконечного пространства, происходит максимальное усиление волн в три раза:

(8)       \(A_{\max}^{\text{(mod)}} = 3a = 3\sqrt{E}\),

где E — энергия (6), запасенная несущей волной, как и ранее. Именно такой бризер изображен на рис. 11. Он носит собственное имя — бризер Перегрина⁵. Его аналог, но уже полученный в результате численного моделирования полных трехмерных уравнений гидродинамики, показан на рис. 12. Выросшая из почти однородного цуга волна настолько крутая, что в следующие моменты времени она обрушивается.

Рис. 12. Волна-убийца, возникшая в результате развития модуляционной неустойчивости, по результатам численного моделирования уравнений гидродинамики (нормированные оси)

В 2000-х годах самомодуляция волн на глубокой воде была предложена теоретиками как наиболее вероятный претендент на физический механизм возникновения волн-убийц, не требующий выполнения экзотических условий. Сравнивая формулы усиления волн в результате линейного сложения (7) и нелинейной самомодуляции (8), можно прийти к выводу: если для модуляционной неустойчивости максимально возможное усиление в три раза достигается в случае сбора энергии волн с бесконечного интервала⁶, то такое же усиление происходит при линейной суперпозиции всего девяти гармоник с одинаковой амплитудой. Совпадение фаз большего числа волновых компонент (N > 9) может привести к еще большему усилению. Значит ли это, что механизм случайного линейного сложения волн обладает более значительной способностью генерировать волны-убийцы, чем модуляционная неустойчивость? Видимо, нет.

Модуляционная неустойчивость: что в индексе тебе моём

Эффект нелинейной самомодуляции волн не укладывается в рамки предположения о независимости гармоник, составляющих волновое поле (3), ведь гармоники согласованно обмениваются энергией. Потому и модельное распределение Рэлея (2) становится неприменимым. Как следует из теоретических прогнозов и многочисленных вычислительных и лабораторных экспериментов, которые были выполнены за последние 20 лет, эффект модуляционной неустойчивости приводит к существенному повышению вероятности образования экстремальных волн в условиях достаточно больших глубин.

Задача модуляционной неустойчивости не одной гармоники, а сразу большого их набора (спектра), как происходит в реальном море, оказывается куда более сложной для анализа. Однако можно предложить довольно простой параметр, определяющий выполнение условий модуляционной неустойчивости, который полностью вычисляется по данным спектра. Запишем его условно в форме

(9)       \(\text{BFI} \sim \frac{\text{крутизна волн}}{\text{ширина спектра}}\).

Величина BFI (Benjamin—Feir Index, или индекс модуляционной неустойчивости) пропорциональна отношению двух безразмерных параметров: крутизны волн (ее можно определить как произведение амплитуды волны на волновое число — k₀a) и относительной ширины спектра (характерной ширины функции волновых чисел — a_k). Для возникновения неустойчивости волн должно выполняться условие BFI > 1. Потому для заданной крутизны волн широкие спектры устойчивы, а узкие подвержены модуляционной неустойчивости. У индекса модуляционной неустойчивости есть прозрачный физический смысл: он характеризует отношение эффектов нелинейности к эффектам дисперсии. В нелинейной оптике существует схожий параметр надкритичности, а для волн на мелкой воде — параметр Урселла.

Индекс BFI (9) обсуждался в статье И. Альбера [15] в приложении к реальным морским условиям. Типичные морские спектры оказались модуляционно устойчивыми, потому эффект самомодуляции поверхностных волн долгие годы считался не играющим в настоящем море никакой роли. Отметим, однако, что поскольку характеристики спектров были близки к условию нейтральной устойчивости, Альбер предположил возможную ограничивающую роль модуляционной неустойчивости. Под ее действием узкие спектры быстро уширяются (как мы обсуждали выше), а потому и не обнаруживаются в результате прямых измерений, которые используют усреднение больших массивов данных. Из таких рассуждений следует, что, хотя узкие спектры и возникают в море нечасто, именно они и представляют наибольший интерес. При них реализуются «аномальные» условия волнения.

Параметр BFI был «переоткрыт» в приложении к морским волнам в самом начале 2000-х годов, и в наше время предпринимаются попытки его практического использования. В частности, он уже рассчитывается Европейским бюро прогноза погоды ECMWF (European Centre for Medium-Range Weather Forecasts). Успешный пример его применения можно видеть на рис. 13, где области больших значений BFI хорошо совпадают с картой повышенной вероятности образования высоких волн. Критерий модуляционной неустойчивости двух скрещенных волновых систем оказался выполненным во время вышеупомянутого инцидента с лайнером «Louis Majesty» [17]. Однако пока применение индекса BFI встречается с трудностями: процедуры его вычисления слишком чувствительны к малым изменениям входных данных, и получаемые карты больших значений BFI в целом довольно плохо соотносятся с прямыми измерениями экстремальных волн буями.

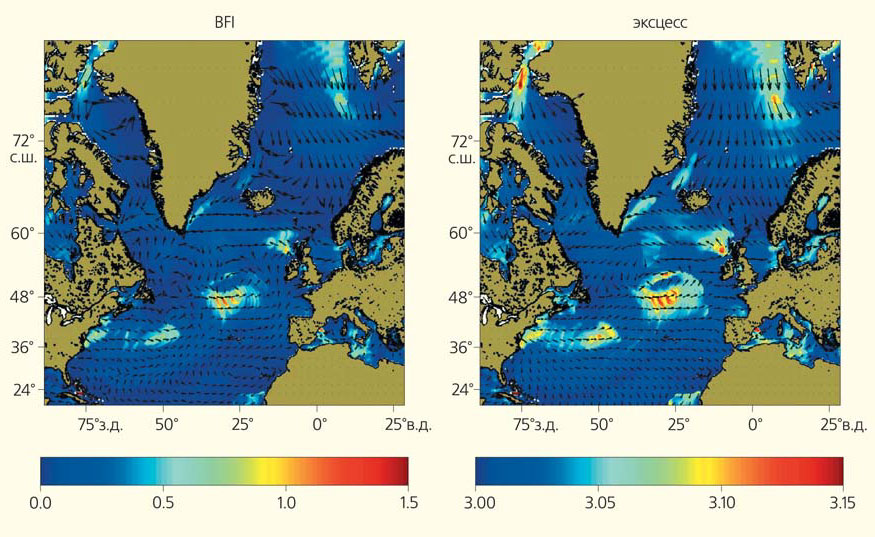
Рис. 13. Пример сопоставления карты рассчитанных индексов BFI (слева) и четвертого статистического момента (эксцесса), характеризующего долю высоких волн (справа), для района Северной Атлантики [16]

Вездесущие солитоны и кто плавает в оптических морях

Про солитоны мы уже упоминали выше. Какую роль они играют в нашей истории? Имя «солитоны» впервые получили в 1960-х годах волны трансляции, обнаруженные Дж. С. Расселом (1834) на поверхности канала вблизи Эдинбурга. Позднее солитонами стали называть уединенные структурно устойчивые волны, возникающие в разных физических задачах и уравнениях, и выглядеть они могут по-разному [18]. Рассел наблюдал мелководный солитон в виде одинокого колокольчика, бегущего без изменения формы. В отличие от «обычных» волн, длина солитона однозначно связана с его высотой (баланс эффектов дисперсии и нелинейности). Солитоны длинных волн можно видеть у кромки воды: подходящие к берегу волны на мелководье становятся непохожими на синусоидальные, они близки по форме к солитонам Рассела и обычно небольшие по высоте (рис. 14). Солитоны катастрофических размеров могут наблюдаться среди лидирующих волн цунами в определенных акваториях. Солитоны также обычное явление для волн, распространяющихся в толще неоднородного по плотности океана. Хоть и почти невидимые на поверхности, такие волны могут достигать амплитуды более сотни метров и приводить к размытию опор океанических платформ и гибели подводных лодок⁷.

Рис. 14. Подходящие к берегу длинные волны приобретают форму солитонов. Фото И. И. Диденкуловой

Солитоны представляют собой уединенные волны, и потому они могут подбегать к наблюдателю незаметно. Подобные события отмечались в литературе среди случаев волн-убийц. Исследовательское судно «Ballena» в 2000 г. было опрокинуто неожиданно высокой волной у берегов Калифорнии на глубине 9 м. Экипаж заметил волну еще на расстоянии около 3 км, но ничего не успел предпринять. Вероятно, заметную роль в генерации таких волн играют двигающиеся по мелководью корабли. В отличие от обычных корабельных волн, солитоны могут распространяться с сохранением значительной амплитуды на большие расстояния.

Здесь мы хотим поговорить о других солитонах, которые могут возникать на достаточно глубокой воде в форме цугов волн, потому называются солитонами огибающей. Склонность волн к существованию в открытом океане группами давно и хорошо известна, достаточно вспомнить картину И. К. Айвазовского «Девятый вал». Связь между солитонами огибающей и группами морских волн подразумевалась в теории и раньше, но никак не использовалась на практике. То, что на поверхности воды могут существовать солитоны огибающей действительно большой амплитуды, выяснилось лишь в последние годы. На рис. 15, а приведены инструментальные записи интенсивного солитона огибающей с разных датчиков по мере его распространения вдоль лабораторного бассейна. А на рис. 15, б, по результатам численного моделирования уравнений гидродинамики построены моментальные профили смещения поверхности. Можно сказать, что солитоны огибающей возникают в результате модуляционной неустойчивости и потому непосредственно связаны с этим механизмом генерации волн-убийц. По некоторым данным, солитоны огибающей были зарегистрированы и непосредственно в открытом океане. На них «вырастали» волны-убийцы. Бризерные решения, приближенно описывающие процесс самомодуляции и затем релаксации волн, сами представляют собой решения солитонного типа. Перечисленные здесь связи между разными элементами волновой динамики в последние годы активно исследуются для описания и прогноза опасных волн. Нелинейность процессов делает динамику нетривиальной, иногда противоречащей интуиции, выработанной на основе наблюдений за «обычными» волнами.

Рис. 15. Солитон огибающей максимальной амплитуды по результатам лабораторных экспериментов (а) и численного моделирования уравнений гидродинамики (б) (в сопровождающей системе координат). Цветными линиями на рис. а показаны записи с 10 датчиков, расположенных вдоль экспериментального лотка, а на рис. б — профили солитона огибающей в два момента времени. Пунктирные линии — огибающие групп [19]

В частности, почему вал именно девятый? В разговорах с европейскими учеными мы встречали упоминание о восьмой самой высокой волне в последовательности групп. Хорошо известен и стал нарицательным случай трех сестер (Glorious Three) — короткой группы волн, столкнувшейся с французским крейсером «Jeanne d’Arc» в 1963 г. [20]. Имеются и другие описания и измерения аномально высоких волн, двигающихся в составе группы (см. рис. 3, 4). Из-за дисперсии на глубокой воде группы движутся со скоростью вдвое ниже, чем сами волны. В результате этого возникает забавный эффект: если стоящая лодка качнется на n прошедших под ней волнах, то на моментальной фотографии окажется лишь n/2 волн (см. рис. 12). Солитоны огибающей обладают всеми свойствами солитонов. В частности, их длина (измеряемая в волнах) связана с их высотой (в терминах крутизны, как было описано выше). Исходя из известных значений наблюдаемой крутизны морских волн, можно сделать теоретическую оценку: в среднем группы интенсивных морских волн должны состоять из примерно 5–7 индивидуальных волн (на моментальном снимке). Получилось довольно неплохое соответствие.

Мы обсуждали выше, как из-за разницы в скоростях распространения волн возможна их фокусировка. Имеет место и обратный процесс: стоит в какой-то момент времени изменить скорость частиц на обратную, тут же фокусировка меняется на дефокусировку. Видео красивого эксперимента по обращению дисперсионного расплывания можно просмотреть в Интернете. Таким образом, дисперсия стремится растащить интенсивную волновую группу, из-за чего максимальная амплитуда волн будет уменьшаться со временем. Нелинейность производит компенсирующий эффект, удерживая форму группы, и в случае солитона сохраняет неизменной максимальную амплитуду волн. Такое объяснение «на пальцах» подсказывает, как обстоятельство существования солитонов огибающей может приводить к изменению вероятности появления волн большой высоты. Отметим сходство максимальной волны, рожденной линейной суперпозицией всех гармоник спектра JONSWAP (см. рис. 9, б) и профиля солитона огибающей в момент максимального гребня (см. рис. 15, б — синяя линия). Если в случае линейной динамики момент совпадения фаз гармоник происходит мимолетно, то в случае солитона огибающей это долгоживущее состояние.

Термин оптическое море стал появляться в научной литературе из-за множественных прямых аналогий между процессами в гидродинамике и нелинейной оптике [22]. В частности, для описания модуляций смещения морской поверхности и модуляций электромагнитного поля в оптическом волокне в первом приближении используются одни и те же уравнения. Солитоны огибающей часто называют оптическими солитонами, они давно изучаются в оптике. Поскольку все процессы в волноводах происходят с огромной скоростью, высказывалась идея о построении требуемых в инженерии вероятностных распределений для очень редких и экстремальных морских волн на основе моделирования эквивалентной оптической системы. К сожалению, эта идея не получила практической реализации, поскольку сходство между нелинейными волнами в оптоволокне и в море лишь приближенное.

Тем не менее сейчас именно в оптических и гидродинамических задачах предпринимаются активные попытки описания сложной нелинейной динамики волн в терминах солитонов. Последние обнаруживаются в полях случайных волн по результатам численного моделирования и экспериментальных измерений с помощью метода обратной задачи рассеяния (так называемого нелинейного метода Фурье), предложенного на рубеже 1960–1970-х годов (в том числе и в пионерных работах российских ученых В. Е. Захарова и А. Б. Шабата). Аппарат этого метода относительно тяжел в использовании [23], но в последние годы появляется все больше работ по его применению. Метод обратной задачи рассеяния можно также использовать для кодировки информации при помощи солитонов, с последующей быстрой дешифровкой. В современном мире оптические волны-убийцы оказываются не менее опасными, чем морские, поскольку способны приводить к электрическому пробою передающих информацию волоконно-оптических линий. Потому в последнее десятилетие особенно активны их исследования в оптических волноводах.

Случайное неслучайно

Мало понимать, почему возникают опасные волны, хочется уметь их предсказывать и избегать. Все известные сегодня системы прогноза ветрового волнения не способны учитывать эффекты, связанные с модуляционной неустойчивостью и возникновением солитоноподобных волновых структур. Используемые модели оперируют со спектрами волн, предполагая, что фазы гармоник всегда случайны и всегда независимы. Большинство моделей дополнительно предполагает медленность происходящих процессов. Бюро погоды выдают прогноз на последующие часы и дни.

Рис. 16. Симуляция прогноза волн по данным радара (численное моделирование морской поверхности, моментальный вид сверху). Желтым контуром показана область измерения подходящих волн, красным пунктиром — контур искусственного подавления волн. Цифрами обозначены контрольные точки [21]

Нам симпатичны рассуждения, приведенные итальянским океанологом Л. Кавальери [24]. В них предлагается представить, что в нашем распоряжении имеется суперкомпьютер, способный рассчитать так много и так быстро, как требуется. При таком совершенном техническом инструменте каковы же физические ограничения предсказания опасных явлений в поле ветровых волн, учитывая их внешне случайный характер? Если допустить, что положение поверхности воды и распределение скоростей жидкости полностью известны в какой-то момент времени (начальные условия), возможен расчет уравнений гидродинамики для последующих времен и тем самым возможен детерминистский прогноз. Сегодня эта задача кажется технически реализуемой для оперативного предсказания волновой обстановки на небольших областях, скажем, в радиусе нескольких километров вокруг корабля. Информация о положении водной поверхности с большой частотой обновления может получаться со специального радара, что довольно хорошо определяет и поля скоростей жидкости, а расчет уравнений гидродинамики для такой области может осуществляться быстрее реального времени на графическом процессоре персонального компьютера (рис. 16). Если расчет на большей акватории — дело техники, то горизонт детерминистского прогноза в несколько минут не может быть преодолен как по причине накопления ошибок (из-за неточных начальных условий, действия таких неучтенных сил, как ветер и др.), так и вследствие собственных свойств решений уравнений гидродинамики как нелинейной динамической системы. Таким образом, если уже осуществляемый неточный прогноз выдается на часы и дни, то идеальный прогноз невозможен даже на час вперед.

Конструктивным путем мог бы стать промежуточный способ описания морских волн и, соответственно, прогноза, в терминах групп волн. Если для предсказания наличия гребня или ложбины волны в конкретном месте и в конкретный момент времени такой подход не годится, то неоднородность распределения волновой энергии по поверхности моря (и, соответственно, высокий шанс возникновения волн большой высоты в конкретной небольшой области в конкретный интервал времени) он смог бы описывать. Упомянутое нами выше нелинейное уравнение Шрёдингера, принадлежащее классу моделей огибающей волн, с некоторой натяжкой можно отнести к такому направлению.

Таким образом, если динамика индивидуальных волн может быть предсказана только на короткое время, то поведение групп — на несколько большее. Для еще более далеких горизонтов прогноза (более тысячи периодов, что соответствует 2–3 ч) принципиально возможно только усредненное вероятностное описание, в том виде, в каком оно существует сегодня. Для него насущная задача — учет аномальных состояний моря с высокой вероятностью появления волн-убийц. Один из предлагающихся способов усовершенствования прогноза заключается в замене используемых спектральных (уже усредненных по фазам) эволюционных моделей на детерминистские эволюционные уравнения с последующим усреднением результатов вычисления (так называемое прямое численное моделирование, или метод Монте-Карло). Такие пробные расчеты уже проводились для модельных случаев, они требуют намного больших вычислительных ресурсов.

Рис. 17. Фотография морской поверхности с наложенной картой величин смещения поверхности (цветная шкала справа), определенных по данным стереометрии [25]

Среди современных направлений исследований морских волн, которые стали возможными благодаря совершенствованию технических средств, следует отметить стереометрические способы измерения, которые позволяют получать намного более полную информацию о волнах. Пример обработки одного кадра съемки таким способом приведен на рис. 17. Поясним, зачем это нужно, помимо очевидного интереса к трехмерным формам экстремальных волн. Как упоминалось выше, в большинстве случаев информация о волнах представлена спектром — распределением энергии волн по частотам или волновым числам. Такое представление кроме осреднения по фазам содержит осреднение по направлениям волн, а также предполагает однозначную линейную связь между частотой и волновым числом, что в действительности выполняется лишь приближенно. Стереометрические измерения волновой поверхности позволяют получать распределения энергии волн по частотам и волновым векторам одновременно. Графически такие данные можно представить в виде трехмерных проекций четырехмерных графиков (две компоненты волновых векторов, частота и спектральная энергия). Из них возможно получать информацию о направлении движения волн, степени их нелинейности, наличии течений и др. Уже существующие сегодня установки позволяют измерять трехмерные волны непосредственно в открытом океане. Такие регистрации принципиально отличаются от ранее использовавшихся в океанографии мареограмм и требуют как развития новых методов обработки, так и теоретических исследований. На сегодня не унифицирован даже способ определения высоты таких волн. Описание эволюции трехмерных волн даст максимум информации.

Здесь мы постарались в простой форме рассказать о физической проблеме волн-убийц и о пути к ее решению. Для дальнейшего чтения можно порекомендовать наши монографии [26, 27]. Свежий обзор на более серьезном уровне «Морские волны-убийцы: наблюдения, физика и математика» должен появиться в журнале «Успехи физических наук» [28].

Исследования поддержаны Российским научным фондом (проект 19-12-00253) и Российский фондом фундаментальных исследований (проекты 19-55-15005 и 21-55-15008).

Литература / References

1. Лопатухин Л. И., Бухановский А. В., Дивинский Б. В., Рожков В. А. О необычных волнах в океанах и морях. Научно-технический сборник Российского морского регистра судоходства. 2003; 26: 65–73. [Lopatukhin L. I., Bukhanovsky A. V., Divinsky B. V., Rozhkov V. A. About unusual waves in the oceans and seas. Scientific and technical collection of the Russian Maritime Register of Shipping. 2003; 26: 65–73. (In Russ.).]

2. Лопатухин Л. И. Ветровое волнение: Учеб. пособие. СПб., 2012. [Lopatukhin L. I.Wind Waves: Textbook. St. Petersburg, 2012. (In Russ.).]

3. Akhmediev N., Ankiewicz A., Taki M. Waves that appear from nowhere and disappear without a trace. Physics Letters. 2009; 373: 675–678.

4. Диденкулова Е. Г., Пелиновский Е. Н. Волны-убийцы в 2011–2018 годах. Доклады РАН. Науки о Земле. 2020; 491: 97–100. [Didenkulova E. G., Pelinovsky E. N. Freak Waves in 2011–2018. Doklady Earth Sciences. 2020; 491: 187–190.]

5. Didenkulova E. G. Catalogue of rogue waves occurred in the World Ocean from 2011 to 2018 reported by mass media sources. Ocean and Coastal Management. 2020; 188: 105076.

6. Кузнецов К. И., Зайцев А. И., Костенко И. С. и др. Наблюдения волн-убийц в прибрежной зоне о.Сахалин. Экологические системы и приборы. 2014; 2: 33–39. [Kuznetsov K. I., Zaitsev A. I., Kostenko I. S. et al. Observation of the freak waves in the coastal zone of the Sakhalin Island. Environmental systems and devices. 2014; 2: 33–39. (In Russ.).]

7. Glein J., Kumar V. S., Balakrishnan N. T. M. et al. Freak waves off Ratnagiri, west coast of India. Indian Journal of Geo-Marine Sciences. 2011; 43: 1339–1342.

8. Горский Н. Н. Тайны океана. Под ред. В. П. Зенковича. М., 1968. [Gorsky N. N. Secrets of the Ocean. V. P. Zenkovich (ed.). Мoscow, 1968. (In Russ.).]

9. Лавренов И. В. Встреча с «волной-убийцей». Морской флот. 1985; 12: 28–30. [Lavrenov I. V. Meeting with the «killer wave». Marine fleet. 1985; 12: 28–30. (In Russ.).]

10. Лавренов И. В. Математическое моделирование ветрового волнения в пространственно-неоднородном океане. Под ред. И. Н. Давидана. СПб., 1998. [Lavrenov I. Wind-Waves in Oceans. Dynamics and Numerical Simulation. Springer, 2003.]

11. Cattrell A. D., Srokosz M., Moat B. I., Marsh R. Can rogue waves be predicted using characteristic wave parameters? Journal of Geophysical Research: Oceans. 2018; 123: 5624.

12. Christou M., Ewans K. Field measurements of rogue water waves. Journal of Physical Oceanography. 2014; 44: 2317–2335.

13. Liu P. C., MacHutchon K. R. Are there different kinds of rogue waves? Proceedings of the 25th Int. Conf. OMAE 2006. Hamburg, 2006; 92619.

14. Zakharov V. E., Ostrovsky L. A. Modulation instability: the beginning. Physica D. 2009; 238: 540–548.

15. Alber I. E. The effects of randomness on the instability of two-dimensional surface wavetrains. Proc. Roy. Soc. Lond. A. 1978; 363: 525–546.

16. Leon S. P. de, Soares C. G. Extreme wave parameters under North Atlantic extratropical cyclones. Ocean Modelling. 2014; 81: 78–88.

17. Cavaleri L., Bertotti L., Torrisi L. et al. Rogue waves in crossing seas: The Louis Majesty accident. Journal of Geophysical Research: Oceans. 2012; 117: C00J10.

18. Филиппов А. Многоликий солитон. М., 1985. [Filippov A. The Many-Faced Soliton. Moscow, 1985. (In Russ.).]

19. Slunyaev A., Clauss G. F., Klein M., Onorato M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids. 2013; 25: 067105.

20. Дьяченко А. И., Захаров В. Е., Шамин Р. В., Бадулин С. И. Волны-убийцы и задачи их исследования. Мировой океан. Под ред. Л. И. Лобковского. М., 2013; 1: 576–592. [Dyachenko A. I., Zakharov V. E., Shamin R. V., Badulin S. I. Killer waves and the tasks of their study. World Ocean. L. I. Lobkovsky (ed.). Moscow, 2013; 1: 576–592. (In Russ.).]

21. Simpson A., Haller M., Walker D. et al. Wave-by-wave forecasting via assimilation of marine radar data. Journal of Atmospheric and Oceanic Technology. 2020; 37: 1269–1288.

22. Dudley J. M., Genty G., Mussot A. et al. Rogue waves and analogies in optics and oceanography. Nature Reviews Physics. 2019; 1: 675–689.

23. Захаров В. Е., Манаков С. В., Новиков С. П., Питаевский Л. П. Теория солитонов. Метод обратной задачи. М., 1980. [Novikov S. P., Manakov S. V., Pitaevskii L. P., Zakharov V. E. Theory of Solutons: the Inverse Scattering Method. Consultants Bureau. N.Y., 1984.]

24. Cavaleri L. Wave modeling: Where to go in the future. Bulletin of the American Meteorological Society. 2006; 87: 207–214.

25. Bergamasco F., Torsello A., Sclavo M. et al. WASS: An open-source pipeline for 3D stereo reconstruction of ocean waves. Computers & Geosciences. 2017; 107: 28–36.

26. Kharif C., Pelinovsky E., Slunyaev A. Rogue Waves in the Ocean. Springer, 2009.

27. Куркин А. А., Пелиновский Е. Н. Волны-убийцы: факты, теория, моделирование. М.; Берлин, 2016. [Kurkin A. A., Pelinovsky E. N. Freak waves: facts, theory, modeling. Moscow; Berlin, 2016. (In Russ.).]

28. Слюняев А. В., Пелиновский Д. Е., Пелиновский Е. Н. Морские волны-убийцы: наблюдения, физика и математика. Успехи физических наук. 2021. DOI:10.3367/UFNr.2021.08.039038. [Slunyaev A. V., Pelinovsky D. E., Pelinovsky E. N. Rogue waves in the sea: observations, physics and mathematics. Physics-Uspekhi. 2021. 10.3367/UFNe.2021.08.039038.]

¹ В журнале «Природа» уже публиковался наш взгляд на эту проблему. См.: Пелиновский Е. Н., Слюняев А. В. Фрики — морские волны-убийцы. Природа. 2007; 3: 14–23.

² В частности, в детской энциклопедии об опасных природных явлениях «Я познаю мир. Природные катастрофы» (М., 2006) солитонам посвящен отдельный раздел.

³ Произошедший разлив нефти называли худшей экологической катастрофой у берегов Испании.

⁴ Строго говоря, введенная так величина E лишь пропорциональна полной энергии волн при определенных условиях. Но для наших рассуждений это неважно.

⁵ По фамилии первооткрывателя D. H. Peregrine (1938–2007), опубликовавшего в 1983 г. решение в не слишком известном журнале. В 1999 г. и позднее это решение было предложено для описания волн-убийц сразу в нескольких публикациях.

⁶ На самом деле были сконструированы и более сложные аналитические решения, описывающие усиление больше чем в три раза (их иногда называют суперволны-убийцы). Но в данном месте повествования они не играют принципиальной роли.

⁷ См.: Степанянц Ю. А. Могут ли внутренние волны погубить подводную лодку? Природа. 2021; 6: 54–66.