Изобразительная нить: математика

По материалам проекта «Математические этюды»
«Квантик» №5, 2024

Всего лишь натянутые прямые нити, а вырисовывается картина. Такая техника называется изонить (изобразительная нить), вышивка по картону, а по-английски String Art или Сurve Stitching. Эти слова можно встретить и когда говорят о детском творчестве, и когда говорят об искусстве. А читателям «Квантика», интересующимся не только красотой, но и устройством мира, цикл статей «Изобразительная нить» позволит лучше понять физическое явление под названием каустика и его математическую основу — геометрическое понятие огибающая.

Считается, что техника string art как искусство восходит к английским ткачам XVII века, которые, вбивая гвозди в дощечки и в определённой последовательности натягивая нити, делали украшения для дома. Со временем техника утратила популярность, и интерес к ней возродился лишь в середине XIX века, когда Мэри Буль — педагог, автор книг, популяризатор идей, помощница и жена математика и логика Джорджа Буля, предложила использовать старинный вид рукоделия в качестве оригинального способа обучения детей азам математики. Продолжим её начинание.

На сторонах произвольного угла отметим одинаковое количество точек так, чтобы шаг между точками на каждой из сторон был постоянным. Занумеруем их на одной стороне, считая от вершины угла, а на другой стороне — к вершине угла. Если соединить нитями точки с одинаковыми номерами, то увидим... параболу! Ту самую параболу, которая изучается в школе, используется в прожекторах и спутниковых антеннах.

Техника исполнения может быть разной. Можно на краях картона делать прорези, можно просто протыкать дырки посреди листа картона: не зря одно из названий этой техники — «вышивка по картону». А можно вбить гвоздики в фанерную основу или сделать деревянную рамочку с пропилами по краям. Заметим, что параболу можно «сшить» одной нитью, причём на обратной стороне не будет нагромождения — лишь стежки, соединяющие соседние по стороне угла точки.

Удивительно другое. Все линии прямые, нет нити в форме параболы, но мы видим и саму параболу! Мы приходим к важному понятию — огибающей семейства прямых, в рассмотренном случае — касательных к параболе. Кривая называется огибающей бесконечного семейства прямых, если она на всём своём протяжении в каждой точке касается какой-нибудь из прямых, и каждая прямая семейства является касательной к этой кривой. В точках огибающей картинка получается «более закрашенной»: видимая глазом кривая «состоит» из точек касания. Другими словами, возле огибающей получается повышенная «скученность» прямых: возле каждой точки огибающей проходит много прямых-касательных, которые вдали от огибающей расходятся по своим направлениям.

Итак, если мы хотим увидеть гладкую кривую, а изображать разрешается только прямые, надо нарисовать касательные к этой кривой. Так можно получить и ближайших родственников параболы — эллипс и гиперболу: по ссылке «Эллипс, гипербола, парабола: складывание листа бумаги» можно посмотреть красивые анимации.

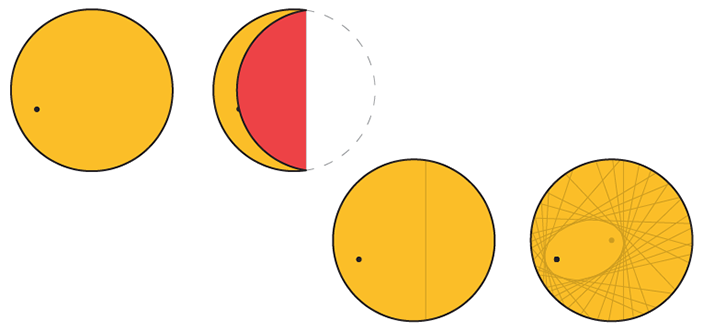
Возьмите бумажный круг и отметьте точку внутри него. Перегибайте круг так, чтобы загнутый край круга каждый раз проходил через отмеченную точку. Сделав так несколько раз, вы увидите, как внутри круга начнёт появляться эллипс, который вырисовывают линии сгиба — касательные к нему. Отмеченная точка круга будет одним из фокусов этого эллипса, а вторым фокусом будет центр бумажного круга.

Для построения гиперболы приклейте бумажный круг скотчем к листу бумаги. Складывайте круг к точке, отмеченной вне него. Линии сгиба «нарисуют» гиперболу, у которой отмеченная точка будет фокусом, а вторым фокусом будет центр бумажного круга.

Вернёмся к параболе. Возьмите обычный прямоугольный лист бумаги и недалеко от его стороны отметьте точку. Складывайте лист по различным направлениям так, чтобы эта сторона всегда проходила через отмеченную точку. Огибающая сгибов — парабола. Фокусом параболы является отмеченная точка, а директрисой — использованный край листа бумаги.

Читатель может задать резонный вопрос: почему для эллипса и гиперболы требуется окружность (круг), а для параболы — нет? На самом деле в случае параболы окружность тоже присутствует, только бесконечно большого радиуса — в виде прямой, края листа бумаги. Родственный факт: у эллипса и гиперболы по два фокуса, а у параболы — один.

Используя уже понятную читателю технологию вышивки по картону, можно создавать и художественные произведения. В качестве примеров из интернета: лодочка-трапеция с парусом-треугольником и парусом-параболой (справа), параболы в квадрате и в окружности (ниже).

В заключение отметим, что бывает и другой подход к созданию изображений из нитей, который сейчас довольно популярен для изготовления подарков на основе grayscale-изображений. При нашем подходе с помощью нитей-касательных вырисовывалась гладкая кривая или граница области, ограниченной несколькими кривыми, а в упомянутой технологии положение нитей подбирается так, чтобы их пересечения приближали серость областей исходного изображения. Тут для расчёта расположения нитей тоже используется математика, но уже другая.

Художник Мария Усеинова

Рисунки: проект «Математические этюды»