Загадочные круги
Сергей Дориченко, Сергей Шашков, Александр Шень
«Квантик»№7, 2023


Об этом любопытном эксперименте нам когда-то рассказал Жак Мазойе, профессор Высшей нормальной школы в Лионе (Франция). Возьмём лист бумаги со случайно расположенными чёрными пятнышками (рис. 1). Сделаем две копии на прозрачной плёнке и наложим друг на друга, глядя на просвет. Если совместить точно — получится исходная картинка. Но если немного повернуть один лист относительно другого (рис. 2), картинка изменится: явно видны окружности. Откуда они возникают, если изначально никаких окружностей не было?

Рис. 2
Одно из возможных объяснений такое. Вторая картинка слегка повёрнута относительно первой. Около центра поворота разница невелика, и картинки практически совпадают (этот участок хорошо виден). Чуть дальше от центра пятнышки уже не совпадают, но накладываются друг на друга, образуя маленькие «дуги» (как показано на рисунке 3).
Эти «дуги» и являются частями окружностей, которые мы видим. По этой теории, окружности должны быть видны на таком расстоянии от центра, где пятнышки ещё накладываются. Когда пятнышки разъезжаются дальше, окружности постепенно должны перестать быть заметны. Однако мы видим окружности и существенно большего радиуса. Почему? Возможно, чёрные пятнышки, случайно разбросанные по листу, образуют иногда пятна большего размера, поворот которых мы и замечаем. Или мы по инерции видим окружности там, где их уже нет. (В самом деле, если закрыть нижнюю половину рисунка 2, разглядеть окружности в верхней половине будет труднее.)
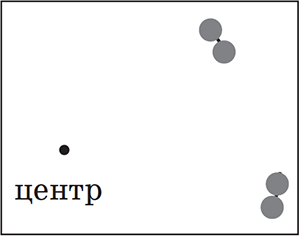
Рис. 3
Но продолжим наши эксперименты. Сдвинем немного одну картинку относительно другой в какую-нибудь сторону. Как ни удивительно, окружности снова будут видны, но центром будет уже другая точка.
Так проявляется замечательное свойство движений плоскости: сделав последовательно поворот и сдвиг, мы в итоге снова получим поворот. Другими словами, когда мы сначала повернули одну картинку, а затем сдвинули её относительно другой, полученный результат точно такой же, как если бы мы просто повернули первую картинку вокруг другой точки. Одно из доказательств можно прочитать в статье Вадима Бугаенко «Движения плоскости и теорема Шаля» в журнале «Квант» №4 за 2009 год.1
Ещё одно интересное наблюдение: если медленно сдвигать уже повёрнутый верхний лист в какую-то сторону, центр поворота будет ехать примерно в перпендикулярном направлении!

Советы по проведению опыта
Весь опыт можно провести онлайн по ссылке Теорема Шаля в интернете, если вы поверите авторам сайта, что они делают то, что утверждают. Если же нет, там можно скачать файл с картинкой для распечатки.
Печатать лучше всего на прозрачной плёнке. Если её нет — на тонкой бумаге, но тогда, когда будете смотреть на круги, подсветите бумагу сзади яркой лампой или приложите к хорошо освещённому окну (фонарик от телефона подходит хуже). Круги будут видны сквозь бумагу и при менее ярком свете, если отзеркалить первую картинку и для совмещения перевернуть верхний лист белой стороной к себе; ссылка для этого варианта.

Если будете сами писать программу, рисующую случайные чёрные пиксели, ставьте их раза в три реже, чем белые (иначе картинка будет слишком чёрной).
Крутить можно, сначала точно совместив картинки, а потом прижав их пальцем в одной точке к оконному стеклу. Но, скорее всего, эффект проявится, даже если просто положить первый лист на второй «чуточку иначе»: ведь как ни двигай лист, не переворачивая, по сути мы его на сколько-то поворачиваем относительно второго и на сколько-то сдвигаем. Важно лишь, чтобы поворот был на ненулевой, но маленький угол, а сдвиг — на маленькое расстояние.
Художник Алексей Вайнер
1 В том же номере был опубликован и первый вариант статьи, которую вы сейчас читаете.



















Рис. 1