Падение магнита в алюминиевой трубке

Александр Князев, Александр Князев (младший)
«Квант» №1, 2021

Демонстрация падения магнитного столбика сквозь толстостенную медную или алюминиевую трубку очень проста, но всегда с восторгом и удивлением воспринимается зрителями. Вначале через такую вертикально расположенную трубку длиной около 1 м и внутренним диаметром 18 мм бросается без начальной скорости кусочек мела или металлический цилиндр. Очевидно, их движение занимает доли секунды. А после этого бросаем в ту же трубку магнитный столбик с длиной и диаметром 15 мм, т. е. примерно равными диаметру трубки. При толщине стенок трубы около 3–4 мм магнитик буквально зависает внутри трубы — движется (без перекоса!) очень медленно, слышен лишь легкий шорох его плавного движения. В нашей демонстрации время падения составляло более шести секунд! В другой демонстрации показывалось замедленное скольжение плоского неодимового магнита по наклонному желобу толстостенного дюралюминиевого уголка.

Физика этого явления довольно ясная, и можно привести наглядные примеры, где этот эффект применяется. Например, в школьных демонстрационных электроизмерительных приборах он используется в конструкции успокоителя стрелки. На конце, противоположном стрелке, укреплена медная пластинка (или плоская медная катушка), которая качается вблизи постоянного магнита. При движении пластинки в ней возникает динамическое электрическое поле и вследствие этого появляются электрические токи (токи Фуко). Взаимодействие этих токов с магнитным полем и тормозит пластинку. Другой, даже более близкий нынешним учащимся пример: магнитный тормоз в винчестере компьютера.

Рис. 1

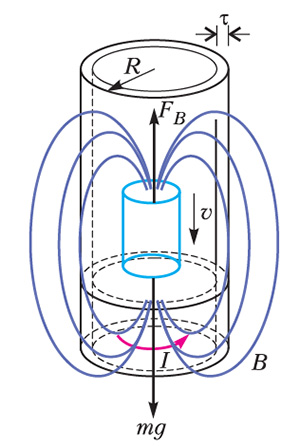
Эффект торможения падающего магнитного столбика хорошо понятен школьникам и описывается в ряде простых задач. Однако никогда не оценивается численно на практических примерах. В данной статье мы показываем, как можно производить численные оценки, когда известных величин немного и добывать необходимые данные приходится самостоятельно¹. Для удобства расчетов будем использовать пример с падением маг-нита в круглой трубке (рис. 1). Движущийся магнит наводит в теле трубки кольцевые индукционные токи. Ток элементарного кольца взаимодействует с магнитом и тормозит его. При этом в момент достижения постоянной скорости сила тяжести магнита уравновешивается магнитной силой.

Сложность численной оценки результатов эксперимента состоит в том, как описать магнитное поле столбика постоянного магнита и как оценить величину наводимых токов. Ясно, что при инженерном конструировании необходимо использовать достаточно сложные формулы, в которых не обойтись без разбиения пространства, занятого проводником и трубкой, на бесконечно малые элементы и дальнейшего интегрирования по ним. Этому учат в университетах и технических вузах. Однако в сложных случаях физики обычно, прежде чем делать расчеты, набрасывают их эскиз — приближенно, но с неплохой точностью получают предварительные результаты, исходя из очень простых соображений. Эти эскизы называются оценками. Физические оценки основаны на понимании сути происходящих процессов, на выделении главных моментов явления. Пожалуй, эти знания прежде всего и необходимы школьникам.

В современной школе иногда решают задачи на расчет электрических полей зарядов и на расчет магнитного поля токов определенной конфигурации (кольцевой ток, ток прямолинейного провода или соленоида), однако совсем нет задач о том, как рассчитывать поля постоянных магнитов. Здесь мы поступим иначе — получим некоторые данные из известной литературы, а остальное необходимое определим экспериментально.

Так, в статьях А.Стасенко из журнала «Квант»² говорится следующее: «...можно попытаться выяснить и характер зависимости силы ... от расстояния. Прежде всего, поймем, как изменяется индукция магнитного поля с удалением от магнита. Будь это точечный электрический заряд, напряженность поля падала бы с квадратом расстояния. Но магнитных зарядов одного знака пока что никто не видел, магнит скорее похож на диполь — два заряда, смещенных относительно друг друга... Можно показать, что оно [электрическое поле] обратно пропорционально кубу расстояния. По аналогии для магнитного поля можно записать \(B\sim \frac{1}{R^3}\)...»

Рис. 2

И в самом деле, подобную формулу для электрического диполя получить совсем нетрудно. При условии, что расстояние между диполями меньше, чем расстояние данной точки от диполя, действительно получим обратную кубическую зависимость. При сравнимых расстояниях формула математически имеет более сложный вид, однако для численной оценки эффекта по порядку величины этого вполне достаточно.

Итак, запишем необходимую зависимость в виде \(B\sim \frac{1}{R^3}\), где коэффициент A для нашего магнита подлежит экспериментальному определению. Для его измерения мы воспользовались простой установкой, ее фотография представлена на рисунке 2, а схема приведена на рисунке 3. Установка состоит из аккумулятора (6 В), амперметра и реостата (12 Ом), которые подключены к подвешенному с помощью штатива на тонких проволочках (h = 500 мм) к отрезку медной проволоки (l = 14 мм, m = 2,7 г). Кратковременно включая постоянный ток через проволоку, мы подносим снизу магнит на расстояние x от 1 до 8 мм (в разных опытах) и сопровождаем его за отклоняющейся проволокой до уравновешения в отклоненном положении, координату отклонения которой обозначим d. В результате проведения эксперимента мы получили следующие значения для модуля индукции магнитного поля: B = 0,2 Тл на расстоянии x = 12 мм от оси цилиндрического магнита и для коэффициента: A = 34 ∙ 10⁻⁸ Тл ∙ м³.

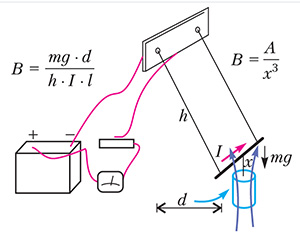
Рис. 3

Для дальнейших расчетов мы воспользовались стандартными формулами, употребляемыми в подобных задачах. Здесь величина магнитной индукции B есть средняя величина продольной составляющей поля магнита в области, охватываемой проводником. Для нашей геометрии считаем ее примерно равной величине поперечной составляющей. Приведем алгоритм наших расчетов:

• ЭДС индукции ξ, наводимая в кольцевом участке трубки, равна \(\xi = - \Phi'=B'(x)\cdot\pi a^2=-\frac{3A}{x^4}\cdot v\cdot \pi a^2\), где а — средний радиус кольцевого участка трубы.
• Ток в кольцевом элементе равен \(I = \frac{\xi }{r}\), где \(r=\rho \cdot \frac{2\pi a}{\Delta l\cdot \tau }\) — сопротивление кольцевого участка трубы, ρ — удельное электрическое сопротивление материала трубки, τ — толщина трубы, Δl — эффективная длина кольцевого участка трубы (в котором возникает основная часть индукционного тока), расположенная в области сильного поля вблизи торцевой части магнита.
• Магнитное поле диполя равно \(B = \frac{A}{R^3}\).
• Сила, действующая на элемент тока со стороны магнита, равна F = 2IB ∙ 2πa. Здесь учтено, что одинаковая магнитная сила действует на верхнем и на нижнем концах цилиндра.
• Условие равномерного движения имеет вид mg = F.

Отсюда искомую установившуюся скорость можно оценить так:

\(v^\ast =\frac{mg(\rho\cdot 2\pi R)}{2\pi ^2B^2R^2s}=\frac{mg\rho \cdot 2\pi R^5}{2\pi ^2A^2s}=-C\frac{mg\rho R^4}{\tau }\),

где s — сечение области протекания тока, τ — толщина трубки, С — общий геометрический коэффициент пропорциональности, получившийся при оценке. В этот коэффициент вошли такие величины, как геометрический размер области с главным кольцевым током (вносящий основной вклад в тормозящую силу), его высота, а также радиус площадки, пронизываемой магнитным потоком. Для численной оценки мы их приняли примерно равными по порядку величин, в противном случае вид формулы стал бы неоправданно громоздким для анализа результата численной оценки. Небольшие различия в численных значениях величин x, Δl, a, d мало будут сказываться на результате, если эти величины имеют численные значения порядка размера магнита d, что вполне соответствует условиям нашего эксперимента.

Примерно по такому же алгоритму можно оценить и эксперимент со скольжением магнита по плоскости, однако выделение геометрического размера главного тока и оценка магнитного поля станут неоправданно сложнее.

В результате мы составили модель явления падения магнитного цилиндра в толстостенной немагнитной (алюминиевой) трубке. Полученная модель позволила оценить скорость падения, которая с удовлетворительной точностью подтвердилась в эксперименте. Видно, что установившаяся скорость действительно пропорциональна массе магнита, обратно пропорциональна толщине трубы и очень сильно зависит от близости магнита к поверхности трубы.

¹ Работа поставлена в Лицее №15 города Саратова учащейся 11 класса У. Маховой. Экспериментальное определение параметров магнита проведено в Физико-техническом лицее №1 города Саратова.

² Это статьи «Любовь и ненависть в мире молекул» («Квант», 1994, №2) и «Как при помощи магнитного поля не дать себя в обиду» («Квант», 1994, №3).