Как из монетки сделать кубик, или Любой жребий за два броска

Григорий Мерзон, Александр Перепечко
(по мотивам Питера Камерона)
«Квантик» №3, 2021

— Кинуть четырёхгранный кубик, и если выпала единица... — бормотал себе под нос Квантик.

— Что ты делаешь? — заинтересовался Ноутик.

— Нашёл настольную игру, а в ней нужно каждый ход кидать четырёхгранный кубик, — пояснил Квантик. — И где я такой достану?

— А пара монеток не подойдёт? У них четыре равновероятных исхода. Если выпало две решки — вот тебе и единица!

— Только одна нашлась. Ну ничего, по два раза буду кидать, — утешился Квантик.

— Если при первом броске выпал орёл, второй раз можно не кидать, — подсказал Ноутик. — На ход будет то один бросок, то два — в среднем полтора! Довольно удобно. А можно с тобой?

— Ага! Та-ак... При игре вдвоём киньте шестигранный кубик, — вновь углубился в правила Квантик. — Боюсь, у меня и такого нет. Но нам нужно лишь проверять, не выпала ли на кубике единица. Может, тоже обойдёмся монеткой?

Можно ли монеткой заменить игральный кубик?

Итак, перед Квантиком встала такая задача:

Монетка при подкидывании выпадает орлом или решкой с одинаковой вероятностью \( \frac{1}{2} \). Можно ли с её помощью получить жребий, выпадающий с вероятностью \( \frac{1}{6} \)?

Нетрудно получить жребий, который выпадает с вероятностью, близкой к \( \frac{1}{6} \). Например, если подкинуть монетку 5 раз, то возможны 2⁵ = 32 различных исхода. Объявим 5 из них «успехом» (то есть жребий выпал), а остальные 27 — «неудачей» (жребий не выпал). Тогда вероятность успеха будет \( \frac{5}{32} \), что лишь чуть меньше \( \frac{1}{6} \). Но кажется, что получить вероятность ровно \( \frac{1}{6} \) при помощи монеты невозможно: ведь для любого выбранного числа успешных бросков вероятность успеха будет равна дроби со знаменателем — степенью двойки.

На самом деле, как уже рассказывал Квантик¹, у таких «невозможных» задач вполне есть решение. Подкинем монетку трижды — возможны 2 · 2 · 2 = 8 исходов. Объявим один из них успехом, пять — неудачей, а в оставшихся двух случаях объявим жребий пока не разыгранным и повторим процедуру. Хоть необходимое число бросков заранее не ограничено, рано или поздно жребий будет разыгран, и вероятность успеха будет ровно в 5 раз меньше вероятности неудачи, то есть равна \( \frac{1}{6} \).

Сколько времени занимает бесконечный процесс?

Хотелось бы, конечно, разыграть жребий побыстрее! Если не будет везти, Квантик может кидать монетку очень долго. А сколько раз ему придётся кидать монетку в среднем?

Первая процедура из трёхкратного подбрасывания монетки будет проведена всегда, то есть с вероятностью 1. Вторая — только если жребий не был разыгран в первой процедуре, то есть с вероятностью \( \frac{1}{4} \). Третья — только если жребий не был разыгран в первых двух процедурах, то есть с вероятностью \( (\frac{1}{4} )^2 \), и т. д.

Поэтому, чтобы найти среднее число процедур (как ещё говорят, математическое ожидание²), нужно вычислить бесконечную сумму \( 1 + \frac{1}{4} + (\frac{1}{4} )^2 + (\frac{1}{4} )^3\:+\:... \)

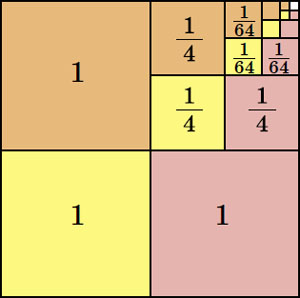
Это можно сделать с помощью картинки³ ниже: разными цветами там закрашены три части квадрата 2 × 2, площадь каждой части равна нашей сумме.

Итак, среднее число процедур равно 4/3, а в каждой процедуре — три подбрасывания, то есть в среднем Квантику потребуется \( \frac{4}{3}\:·\:3 = 4\) подбрасывания монеты.

А нельзя ли побыстрее?

Разыгрывая жребий, мы объявляли успехом 1 исход из 8. Можно сказать, мы начинали с того, что приближали \( \frac{1}{6} \) числом \( \frac{1}{8} \). Но поскольку \( \frac{1}{6} ≠ \frac{1}{8} \), у нас оставались «лишние» исходы (а именно, 2 исхода из 8), после которых мы повторяли процедуру.

Если приблизить \( \frac{1}{6} \) поточнее (скажем, дробью \( \frac{5}{32} \)), жребий будет реже оставаться неразыгранным. Правда, сама процедура начнёт занимать больше времени. Сходу и не скажешь, будет ли это эффективнее.

Попробуйте найти среднее число бросков, если кидать монетку по 5 раз (объявляя 5 исходов успехами, 25 — неудачами, а ещё в двух случаях перекидывая монетку заново). Оказывается, бросков будет ещё больше.

Не будем отчаиваться, а посмотрим внимательнее на исходный алгоритм. Из восьми исходов трёхкратного подбрасывания мы объявили один — успехом, а пять — неудачей. Но ведь у нас есть выбор, каким именно исходам приписывать успех и неудачу — и этой свободой можно воспользоваться.

Будем кодировать исходы тройками ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР, где О — орёл, а Р — решка. Объявим первый исход (ООО) успехом, а 5 последних — неудачей. Ясно, что если первым выпала решка (а это происходит в половине случаев), дальше монету уже можно не кидать! Тогда одна процедура требует не 3 броска, а в среднем \( \frac{1}{2} · 3 +\frac{1}{2} · 1 = 2 \) броска, и весь алгоритм займёт в среднем \( 2 · \frac{4}{3} = 2 \frac{2}{3} \). Уже лучше!

Двух бросков всегда достаточно!

А что делать, если хочется сымитировать жребий с какой-то другой вероятностью успеха x (например, для x = \( \frac{3}{19} \))? Насколько больше потребуется времени, чтобы его разыграть?

Кажется, что чем «сложнее» знаменатель, тем больше нужно бросаний. С другой стороны, увеличивается и простор для оптимизаций.

Удивительно, но всего за два бросания монеты (в среднем) можно сымитировать жребий с любой вероятностью успеха! Для этого разовьём идею экономии бросков из предыдущего раздела, а нужный алгоритм опишем... геометрически.

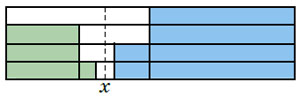
Отметим на отрезке [0;1] точку x. Будем кидать монету, и если выпадает О, будем оставлять от отрезка только левую половину, если выпадает Р — правую, и дальше повторять процедуру (см. рисунок). Подбросив монету N раз, мы придём к одному из 2^N возможных отрезков. Этот отрезок окажется левее x с вероятностью, близкой к x (и тем ближе, чем больше N). Но мы опять можем экономить броски!

Как только у нас остался отрезок, целиком лежащий левее x — мы останавливаемся и считаем, что выпал успех (ведь уже точно получится отрезок левее x), а если остался отрезок целиком правее x, — останавливаемся и считаем, что выпала неудача. Ну а пока оставшийся отрезок содержит x — продолжаем бросать монету.

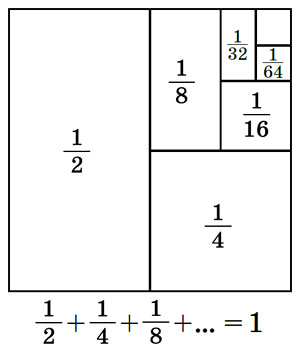
Сколько бросков мы сделаем в среднем? После очередного подбрасывания монеты процесс заканчивается, если мы выбрали тот из отрезков, на котором не лежит точка x. Это обычно происходит с вероятностью \( \frac{1}{2} \) (кроме случая, когда x лежит ровно на границе отрезков — тогда всё точно закончится после этого подбрасывания). Итак, первый бросок потребуется с вероятностью 1, второй — с вероятностью \( \frac{1}{2} \), третий — с вероятностью \( \frac{1}{4} \), и т. д. А всего в среднем потребуется \(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8}\:+\:... = 2 \) подбрасывания монеты (если x попадает на границу одного из отрезков, то даже меньше).

Для знатоков. Можно описать тот же алгоритм и алгебраически. Запишем x в виде бесконечной дроби в двоичной системе счисления. Будем кидать монету, пока впервые не выпадет решка. И если решка выпала на той позиции, где в записи x стоит 1, будем считать, что жребий выпал, если 0 — не выпал.

Например, для \( x = \frac{1}{6} \) получается разложение 0,001010101... — то есть мы кидаем монету пока первый раз не встретится решка, и если на соответствующей позиции в разложении x оказалась 1 (то есть бросков было нечётное число, не равное 1), объявляем жребий выпавшим.

Художник Алексей Вайнер

¹ См. статью Г. Мерзона «1/3, или Две невозможные задачи с решениями», «Квантик» № 6, 2019.

² См. статьи И. Высоцкого и И. Акулича «Новые приключения Стаса», «Квантик» № 3–5, 2016.

³ См. также статью «Картинки вычисляют бесконечные суммы», «Квантик» № 1, 2020.