Франсуа Виет: ученик дьявола

Борис Дружинин
«Квантик» №2, 2021

Начало

Франсуа Виет (François Viète). 1540–1603

Некоторые отучившиеся в школе помнят Франсуа Виета по его знаменитой теореме о свойствах корней приведённого квадратного уравнения. Остальные и это благополучно забыли. А между тем жизнь Франсуа Виета весьма интересна.

Франсуа Виет родился в 1540 году в небольшом городке Фонтене-ле-Конт. Отец Франсуа служил прокурором, и сын намеревался пойти по стопам отца. Учился он сначала в школе при местном монастыре, а затем в университете Пуатье, основанном в 1431 году Карлом VII. По окончании университета в 1560 году получил степень бакалавра, а свою адвокатскую практику начал ещё за год до этого, в 19 лет.

Спустя три года Виет нанялся секретарём к весьма состоятельному господину де Партене. А у господина де Партене была дочь Катрин, которой трудно давалась математика, и Франсуа стал её репетитором. Именно преподавание пробудило в нём интерес к математике, которой он ранее не увлекался. Эта девочка ещё сыграет немаловажную роль в судьбе Франсуа Виета, когда подрастёт, конечно.

Катрин де Партене (1554–1631)

Катрин де Партене вышла замуж и перебралась в Ла-Рошель, а вскоре за ней и Франсуа Виет. В 1571 году Виет поступил на государственную службу в парижский парламент (суд). В столице он завязал знакомства с парижскими математиками. Примерно в это время он написал большую часть «Математического канона» — капитального труда по тригонометрии (опубликован в 1579 году).

При Карле IX Виет был назначен советником парламента Бретани, а при Генрихе III стал уже частным советником короля. После убийства в 1589 году Генриха III перешёл на службу к Генриху Наваррскому, будущему королю Генриху IV. И конечно, всё это время Виет занимался математикой.

Нечистая сила

Виет прославился во времена войны короля Генриха IV с одной стороны и Католической лиги при поддержке Испании с другой стороны. Испанцы знали почти всё о секретных замыслах французов и выигрывали одно сражение за другим. Дело в том, что испанцы изобрели специальный шифр и получали донесения от своих людей во Франции. А перехваченные сообщения французы не могли прочитать.

Король Франции Генрих III. 1551–1589

Шифр был сложным, он состоял из 600 различных знаков, которые иногда менялись. Тогда король обратился к Виету. Много времени провёл Виет за разгадкой шифра и наконец подобрал к нему ключ. И тут же Испания начала терпеть поражения. Испанцы никак не могли понять, в чём дело, пока не узнали, что их шифр разгадал математик Франсуа Виет. Испанские инквизиторы немедленно обвинили Виета в сговоре с нечистой силой: по их мнению, только дьявол мог разгадать такой хитроумный шифр.

Эта история ещё раз доказывает, что для победы нужны не столько пушки и мушкеты, сколько умные образованные люди.

Не было бы счастья

Вернёмся назад. С 23 на 24 августа 1572 года во Франции произошла печально известная во всём мире Варфоломеевская ночь. По разным оценкам, в Париже тогда погибло около 3000 человек, а по всей Франции в погромах было убито около 30 тысяч гугенотов.

Пётр Рамус (Пьер де ла Раме). 1515–1572

В ту ночь погибли муж Катрин де Партене, а также выдающийся математик Рамус (Пьер де ла Раме). Спустя несколько лет Катрин вышла замуж во второй раз. Она отдала руку и сердце принцу де Рогану. Благодаря содействию своей ученицы, Виет в 1580 году получил должность рекетмейстера — докладчика короля по ходатайствам. Он мог от имени короля контролировать выполнение приказов по всей стране! Должность впечатляющая.

В Европе тогда было несколько знатных родов, которые соперничали если не за трон, то за место у трона. И вот в 1584 году представители одного из этих родов Гизы постарались, чтобы Виета отстранили от государственной службы и выслали из Парижа.

Ну что ж, не было бы счастья, да несчастье помогло. Обретя покой и отдых от дворцовой суеты, Франсуа Виет теперь всё своё время мог посвятить математике. Он был убеждён, что существует общая, неизвестная ранее наука, которая могла бы объединить достижения более ранних учёных. И оказался прав!

Именно в этот период учёный изобрёл новую алгебру. Точнее, способ решения алгебраических задач.

Новая алгебра

Огромный вклад в алгебру сделал Диофант ещё в III веке до н. э., используя буквенную символику. Например, уравнение

x³ + 8x − (13x² + 202) = x

Диофант записал бы так¹:

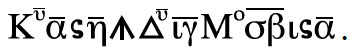
Но у него не было последователей ни среди современников, ни долгое время после. Лишь в конце XV века люди активно занялись разработкой алгебраической символики, а завершили её Виет и Декарт.

До Виета решение каждого уравнения выполнялось по своим отдельным правилам в виде длинных словесных рассуждений и довольно громоздких действий. Даже для записи уравнения требовалось довольно длинное и сложное словесное описание. А на овладение приёмами решений уходили годы.

Виет за время вынужденного «отдыха» основательно изучил труды классиков — дель Ферро, Тартальи, Кардано, Маццоли. Он предложил обозначать неизвестные гласными буквами, а коэффициенты при них — согласными буквами.

Например, уравнение

x³ + 3b²x = 2z³

Виет записывает как

A cubus + B plano 3 in A aequari Z solido 2.

(Степени чисел Виет иногда обозначал иначе, чем степени переменной.) Для уравнений с числовыми коэффициентами обозначения были чуть другими: так, уравнение

x³ − 3x = 1

Виет записывает как

1C − 3N aequatur 1.

Теперь уравнения можно было решать в общем виде, что мы сейчас и делаем.

Знаменитая теорема

Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1615 году. Теперь она носит имя Виета, а сам автор формулировал её так:

Если В + D, умноженное на А, минус А в квадрате равно ВD, то А равно или В, или D.

Доказывается она довольно просто: перепишем данное в условии равенство (B + D)A − A² = BD в виде BA − A² + DA − BD = 0, откуда (B − A)A − D(B − A) = 0. Осталось вынести B − A за скобки: (B − A)(A − D) = 0. Произведение двух чисел равно нулю тогда и только тогда, когда равен нулю хотя бы один из сомножителей, то есть как раз при A = B и при A = D.

Сейчас теорему Виета формулируют иначе:

Сумма корней уравнения x² + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Предшественники

Никколо Тарталья. Ок. 1499–1557

Как это ни странно, но теоремой Виета пользовались ещё до его рождения. Свойства корней приведённого квадратного уравнения понадобились профессору математики из Болонского университета Сципиону дель Ферро и гениальному математику-самоучке Никколо Тарталье. Они первыми в мире, независимо друг от друга, решили в общем виде уравнение третьей степени. Решили, воспользовавшись именно этими свойствами.

Так почему же теорема носит имя Виета? Дело в том, что и дель Ферро, и Тарталья знали её только для квадратного уравнения, а Виет обобщил её на уравнения больших степеней. Он показал, что подобные свойства есть у корней приведённого алгебраического уравнения любой степени

xⁿ + a_n − 1x^n − 1 + a_n − 2x^n − 2 + ... + a₁x + a₀ = 0.

Действительно, если х₁, ..., x_n — различные корни этого уравнения, его можно переписать в виде

(х − х₁)(х − х₂)(х − х₃) ... (х − х_n) = 0,

откуда

a_n − 1 = − (x₁ + х₂ + х₃ + ... + x_n),
a_n − 2 = x₁х₂ + x₁х₃ + ...+ x₁х_n + х₂х₃ + ... + х_n − 1х_n,
a_n − 3 = −(х₁х₂х₃ + х₁х₂х₄ +... + х₁х₂х_n + ...+ х_n − 2х_n − 1х_n),
... ... ...
a₀ = (−1)ⁿх₁х₂х₃ ... х_n.

Геометрия и тригонометрия

Геометрия была первой наукой, применявшейся на практике. Провести границы между земельными участками (геометрия по-древнегречески — ‘измерение земли’), построить храм или просто дом, перекинуть мост через реку — далеко не все случаи, где требуется геометрия. С ней переплетается тригонометрия (по-древнегречески — ‘измерение треугольников’). И геометрия, и тригонометрия применяются практически во всех областях деятельности человека.

Виет вывел формулы синусов и косинусов кратных дуг, полезные в алгебре и геометрии. С их помощью он, например, связал задачу трисекции угла (а также деление угла на 5 равных частей) с решением соответствующего алгебраического уравнения.

А ещё с помощью тригонометрии Виет получил замечательную формулу, выражающую число π через бесконечное произведение:

Гордость Франции

Вот удивительная история, когда Виета выручило глубокое понимание алгебры, геометрии и связей между ними. В 1593 году голландский математик Адриан ван Роумен, известный тем, что нашёл первые 16 знаков числа π, бросил вызов математикам мира. Он разослал во многие страны «страшное» уравнение:

45x − 3 795x³ + 95 634x⁵ − 1 138 500x⁷ + 7 811 375x⁹ − 34 512 075x¹¹ + 105 306 075x¹³ − 232 676 280x¹⁵ + 384 942 375x¹⁷ − 488 494 125x¹⁹ + 483 841 800x²¹ − 378 658 800x²³ + 236 030 652x²⁵ − 117 679 100x²⁷ + 46 955 700x²⁹ − 14 945 040x³¹ + 3 764 565x³³ − 740 259x³⁵ + 111 150x³⁷ − 12 300x³⁹ + 945x⁴¹ − 45x⁴³ + x⁴⁵ = а,

предлагая решить его, к примеру, для

Король Франции и Наварры Генрих IV (1553–1610)

Но во Францию он это уравнение не послал, считая, что там нет математиков, способных его решить. Действительно, Декарт родится только через три года, а Пьера Рамуса не было уже 21 год. Больше всего было ущемлено самолюбие короля Франции Генриха IV. Ему рассказал о вызове голландский посланник, кстати, имевший с собой письмо ван Роумена.

— И всё же у меня есть математик! — воскликнул король. — Позовите Виета!

Франсуа Виет тут же, в присутствии короля, министров и гостей, нашёл один корень уравнения. Король ликовал, все поздравляли придворного советника. На следующий день Виет нашёл ещё 22 корня уравнения. Остальные 22 корня были отрицательными, а таких корней Виет не признавал². Кстати, Виет решил это уравнение первым из получивших.

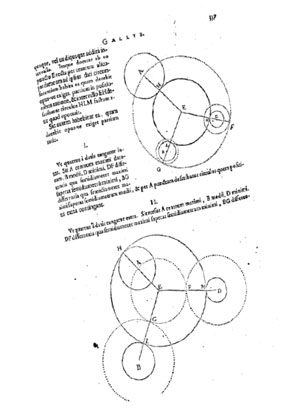
А ещё в ответ он задал задачу Ван Роумену: для трёх данных окружностей построить циркулем и линейкой касающуюся их окружность (задача Аполлония). Сам Виет её решил, а ван Роумен не справился, но с тех пор стал большим почитателем Виета.

Наследие

Виет показал, что алгебраические преобразования можно выполнять не только над конкретными значениями, но и над символами, и тем самым создал понятие математической формулы. Если хотите, Виет «открыл» буквенную алгебру, чем подготовил почву для открытий Декарта, Лейбница, Ферма, Бернулли, Эйлера, Ньютона и других великих математиков.

¹ Подробнее см. книгу: Диофант. Арифметика и книга о многоугольных числах. М.: Наука, 1974.

² Подробнее об этой истории читайте в статье Ю. П. Соловьёва «Вызов Ван Роумена» в журнале «Квант», № 6 за 1986 г.