Драма в облаках

Альберт Стасенко
«Квант» №4, 2019

Рис. 1. Распределение по высоте концентрации молекул — равновесие между энергиями гравитации и теплового хаоса

Древние мудрецы как-то записали: «Темна вода в облацех воздушных», отметив таким образом загадочность происходящих процессов. А эти процессы не только загадочны — они трагичны! Однако, все по порядку.

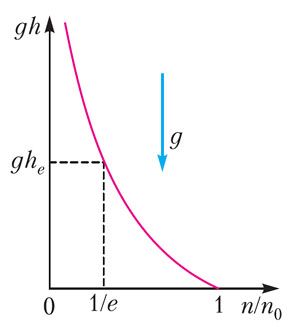
Вспомним одну из важнейших идей термодинамического равновесия. Если есть два энергетических состояния E₁ и E₂, в которых могут находиться участники равновесия при температуре T, то количество этих участников n₁ и n₂ экспоненциально зависит от отношения энергий этих двух состояний и некой характерной энергии теплового хаотического движения kT, а именно: \( n_{1,2}\sim e^{{−}\frac{E_{1,2}}{kT}} \), где k = 1,38 · 10⁻²³ Дж/К — универсальная константа Больцмана. Тут сразу «приходит на ум» распределение молекул массой m по высоте h в изотермической атмосфере (рис. 1):

где g = 9,8 м/с² — ускорение тяготения.

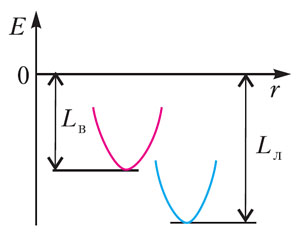
Рис. 2. Удельные энергии испарения (конденсации) и сублимации (плавления) как потенциальные ямы

Применим эту идею к описанию ситуации в облаке, где присутствуют водяные пары, капли воды и кристаллы льда. Прежде всего, как известно, чтобы испарить из водяной лужи (т.е. с плоской поверхности) один килограмм воды, требуется энергия фазового перехода L_в. В расчете на одну молекулу эта энергия равна L_вm. Следовательно, в равновесии отношение концентрации молекул, которых «вытащили из потенциальной ямы» глубиной L_в (рис. 2), к тем, которые остались «на дне» этой потенциальной ямы, равно

Понятно, что для испарения с поверхности замерзающей лужи придется затратить энергию сублимации, превосходящую энергию испарения: L_л > L_в — поскольку для этого надо сначала превратить лед в воду. Значит, показатель экспоненты теперь будет больше, а концентрация пара надо льдом будет соответственно меньше, чем над водой.

Рис. 3. С уменьшением радиуса кривизны капли растет равнодействующая сил поверхностного натяжения

Но капли в чем-то отличаются от лужи: они характеризуются радиусом кривизны a. Согласно понятию поверхностного натяжения, силы взаимодействия всех молекул капли в ее внешнем слое сжимают каплю тем сильнее, чем меньше a. На рисунке 3 сравниваются две капли — побольше и поменьше; видно, что равнодействующая сил поверхностного натяжения, приложенных к одинаковым площадкам на их поверхности, растет с уменьшением a. Это, конечно, сказывается на росте давления в капле и в окружающем паре. Оказывается, над выпуклой поверхностью плотность насыщенного пара выше, чем над плоской поверхностью. Чтобы пояснить это утверждение, рассмотрим сообщающиеся сосуды — один широкий, другой узкий радиусом a (рис. 4, а; здесь изображены два узких сосуда радиусами a₁ и a₂). Будем считать, что стенки сосудов не смачиваются водой. Тогда поверхность воды в капилляре (в узком сосуде) будет выпуклой, а уровень воды будет ниже плоского уровня на \( h = \frac{2σ}{ρ_Вga} \), где σ — коэффициент поверхностного натяжения. Если закрыть сосуды сверху крышкой, то вскоре пар во всем объеме станет насыщенным и будет находиться в состоянии равновесия со своей жидкостью. При не очень малом а плотность пара можно считать постоянной, и давление пара над выпуклой поверхностью будет больше давления над плоской поверхностью на величину

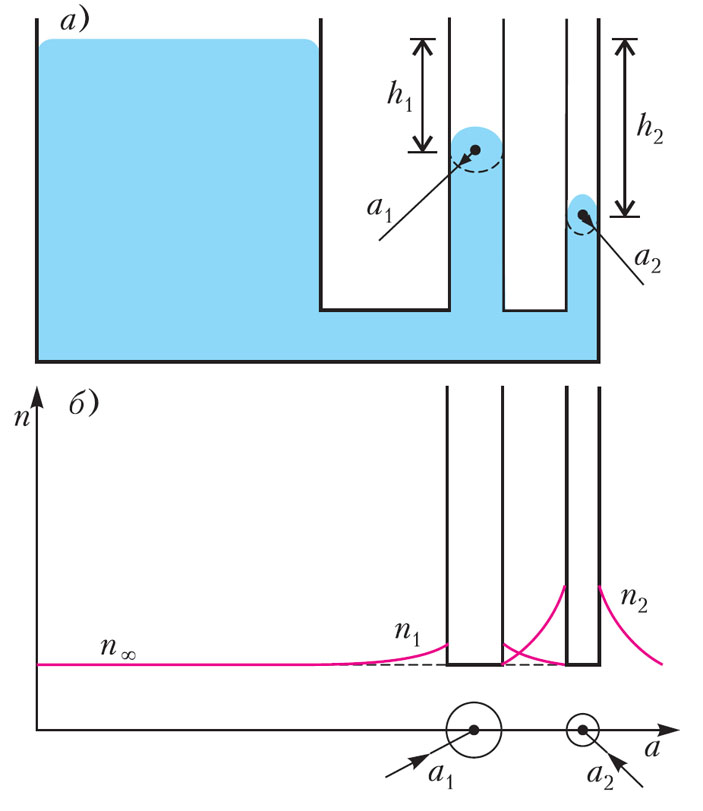
Рис. 4. а) Высота опускания несмачивающей жидкости в капилляре зависит от его радиуса. б) Равновесная концентрация пара зависит от радиуса кривизны капли

Если же а очень мало (∼10⁻⁷ м), то для расчета разности давлений надо использовать формулу Больцмана:

И что же получается — давление и концентрация пара над большей каплей воды меньше, чем над меньшей (рис. 4, б), значит, молекулы пара будут диффундировать через воздух (вспомним и о нем) от малой капли к большой, конденсируясь на последней и увеличивая ее массу. Поистине, как говорили древние мудрецы, «кто имеет, тому дано будет и приумножится, а кто не имеет, у того отнимется и то, что имеет».

Результат известен — падение! Причем, чем крупнее капля, тем труднее ей удержаться в восходящем потоке воздуха: сила тяжести пропорциональна кубу размера, а поддерживающая аэродинамическая сила — квадрату. Возникающая при этом разность скоростей приводит к тому, что большие капли, сталкиваясь с мелкими и объединяясь с ними, растут еще быстрее. Облако разрушается — на земле выпадают осадки!

Ситуация становится еще более драматичной, когда на сцене появляются кристаллы. Поскольку L_л > L_в и давление над их поверхностью меньше, чем над жидкостью, они нещадно поглощают и большие и малые капли. Укрупняясь до размеров, которые уже невозможно поддерживать в восходящих потоках воздуха, кристаллы выпадают вниз, образуя в достаточно плоских облаках «дыры» (рис. 5) — редкое, но яркое явление, которое впечатлительные наблюдатели приписывают инопланетным пришельцам. Этот процесс назван по имени его исследователей явлением (механизмом, эффектом, теорией) Вегенера — Ленгмюра — Бержерона — Финдайзена.

Рис. 5. Дыры в облаках

Конечно, в этом наброске не уделено должного внимания воздуху, в котором и рассматриваются драматические события. А чтобы добавить свою фамилию к приведенной выше замечательной плеяде исследователей, нужно разобраться в явлениях подробнее, поступив в Московский физико-технический институт, например на факультет аэромеханики и летательной техники.