Об укладке блинов, котлет и апельсинов
Сергей Дориченко
«Квантик» №4, 2020
Сегодня Квантик решил серьёзно попрактиковаться в готовке. Сам он обычную пищу не ел, но друзей любил порадовать чем-нибудь вкусненьким.
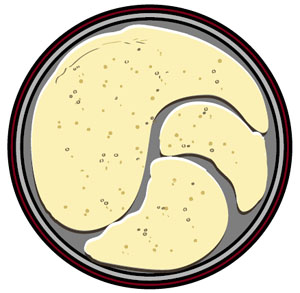
— Начнём с блинов, — решил Квантик.
С тестом проблем не возникло, но первый же блин так причудливо растёкся по сковороде, что явно налез бы на другие блины после переворачивания (рис. 1).
— Интересно, а поместятся ли блины, если я переверну их все?
Квантик любил сначала всё продумать, а потом уже делать. Зачем пытаться укладывать перевёрнутые блины, если они, может, и не влезут? Сначала надо доказать теорему! Но запах подгорающего теста заставил Квантика действовать: он схватил такую же, но холодную сковороду и ловко опрокинул туда все блины, чтобы пока спокойно подумать. Чуть прилипшие блины перевернулись в воздухе целиком вместе с горячей сковородой, но тут же отлипли и аккуратно упали на холодную — румяной стороной кверху.
— Кажется, это было доказательство, — осенило Квантика. — Интересно, а если бы моя сковорода была треугольной? Для равностороннего треугольника всё бы сработало, а вот для любого... пожалуй, не всегда. (А вы поняли, почему?)
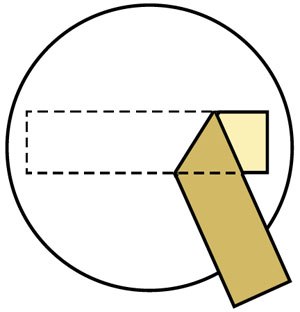
Рис. 2
Следующий блин Квантик сделал «математическим», в виде прямоугольника. Переворачивая его на другую сторону, Квантик немного не рассчитал, и прямоугольник завернулся, да так, что даже вылез за пределы сковороды (рис. 2).
— Надо его хотя бы сдвинуть целиком на сковороду. Ой, а вдруг не влезет?
Времени на доказательство не было, и мысли в голове Квантика сменялись с бешеной скоростью.
— И зачем мне понадобился блин именно в форме прямоугольника? А для другой формы понятнее, что ли, поместится ли загнутый блин? Может, это вообще от формы блина не зависит... Ну если не зависит, то любой, даже самый большой блин должен поместиться, если его загнуть. Стоп, самый большой блин — это же... вся сковорода! Но для неё ответ очевиден!
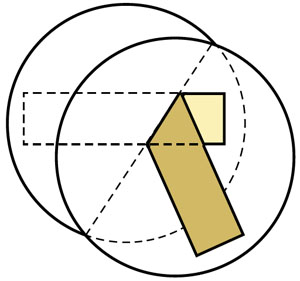
Рис. 3
Квантик от неожиданности резко вдвинул блин на сковороду и погасил огонь. — Ну конечно. Если загнуть по прямой блин размером со сковороду, меньшая часть целиком окажется внутри (под или над) большей, и загнутый блин точно влезет на сковороду! А если взять блин поменьше, он влезет после загиба и подавно (рис. 3).
Квантик решил, что хватит с него на сегодня блинов. Лучше сделать что-нибудь простое и понятное — вот, например, котлеты. Причём круглые и абсолютно одинакового размера.

Рис. 4
Приготовив фарш, Квантик быстро налепил котлет и стал как попало выкладывать их на разогретую сковороду. После шестой котлеты он обнаружил на столе оставшуюся седьмую, места для которой с виду уже не было. Квантик быстро сдвинул котлеты вплотную друг к другу и втиснул седьмую на край — получилось «тютелька в тютельку» (рис. 4).
— Повезло? Или если 6 влезло, то и 7 влезет? — задумался Квантик. Пока котлеты жарились с одной стороны, он аккуратно сформулировал гипотезу.
Котлетная теорема
Пусть на круглой сковороде удалось поместить 6 одинаковых круглых котлет. Тогда на эту сковороду поместится и добавочная седьмая такая же котлета (возможно, для этого придётся передвинуть предыдущие).

— Вроде бы ясно, что расположение в виде «ромашки», когда одна котлета в центре, а остальные вокруг, самое выгодное. Но как это доказать? Если одна котлета лежит точно по центру и есть место ещё хоть для одной, то остальные шесть влезут — просто подряд по кругу. А если никакая котлета не лежит строго по центру? Никаких идей...
Квантик перевернул котлеты, думая дальше.
— Зайдём с другой стороны: какая сковорода нужна для 7 котлет? Радиус котлеты, скажем, 1. Тогда для «котлетной ромашки» хватит сковороды с радиусом 3. Идея! Докажем, что если 6 котлет поместилось, то радиус сковороды не меньше 3.
Квантик убавил газ и накрыл котлеты крышкой.
— И что дальше? Надо как-то использовать, что котлеты не накладываются друг на друга. Ага, это значит, что расстояние между любыми двумя центрами котлет не меньше 2. А ещё котлеты не вылезают за пределы сковороды — то есть расстояние от её края до центра любой котлеты не меньше 1. Иными словами, центры котлет лежат в круге радиуса на 1 меньше, чем у сковороды. Переформулируем-ка задачу:
Точки в круге
В круге лежат 6 точек, расстояния между любыми двумя из них не меньше 2. Тогда и радиус круга не меньше 2.
— Попробовать от противного? — размышлял Квантик. — Пусть радиус круга меньше 2. Случай, когда какая-то точка в центре круга, разобран. А если все точки не в центре, а где-то вокруг? Соединю-ка их с центром.
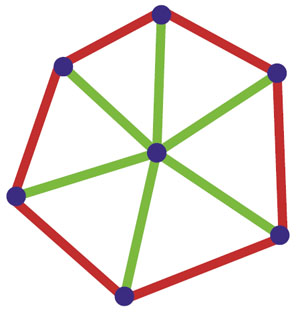
Рис. 5
Квантик погасил огонь, взял бумажку и карандаши и провёл из центра круга шесть зелёных отрезков. Потом подумал немного и соединил «соседние» точки красными отрезками (рис. 5). Получилось 6 треугольников.
— Все зелёные отрезки короче 2. А все красные — не меньше 2. Тогда в каждом из шести треугольников красная сторона — самая длинная. А это значит...
Квантик чувствовал, что решение где-то совсем рядом. И тут он вспомнил, что в треугольнике против большего угла лежит большая сторона.
— ...это значит, что в каждом треугольнике угол против красной стороны строго самый больший. Тогда он по величине больше трети от суммы углов — от 180° — то есть больше 60°. Стоп-стоп-стоп! Шесть углов по кругу — и каждый больше 60°? Выходит, их сумма больше 360° — больше полного оборота! Противоречие!!!
Квантик, решив задачу, никогда не мог сразу остановиться. Вот и сейчас он ещё какое-то время размышлял над последним шагом решения.
— А если бы радиус круга равнялся 2? Тогда красная сторона в каждом треугольнике снова самая длинная, но уже не строго — она может и равняться зелёным. Значит, угол против неё не меньше 60°. А раз сумма шести таких углов равна 360°, все они по 60°. То есть точки лежат на границе круга в вершинах правильного шестиугольника!
Квантик сформулировал доказанный факт:
Вторая котлетная теорема
Если на сковороде радиуса 3 лежат 6 котлет радиуса 1, возможны два случая. Первый: одна котлета лежит точно по центру, а остальные — по краям, касаясь центральной. Второй: 6 котлет лежат «ромашкой» с пустым центральным местом.

Рис. 6
После всех этих котлетных теорем надо было передохнуть, и Квантик решил потренироваться в украшении стола. Он поставил на стол блюдо для фруктов — разумеется, математическое, в форме равностороннего треугольника — и стал выкладывать на него апельсины: тоже математические, то есть абсолютно круглые и одинаковые. Апельсинов было 9, и на блюде осталось место ещё ровно для одного, которого, увы, не было (рис. 6).
— Некрасиво, — подумал Квантик. — Переложу-ка по-другому, чтобы нехватка не бросалась в глаза.
Квантик долго укладывал апельсины в один слой и так, и эдак, и наконец пришёл к тому, что верна
Апельсинная теорема
Если блюдо в виде равностороннего треугольника рассчитано ровно на 10 апельсинов (в один слой, вплотную друг к другу и краям), то, как туда ни клади 9 апельсинов (в один слой), обязательно останется место и для десятого, даже если не сдвигать остальные.
— Вот тебе и отдых, — вздохнул Квантик. — Как подступиться к доказательству — совершенно неясно. Когда на блюде 10 апельсинов, они — вернее, их центры — образуют красивую треугольную решётку. Но почему и 9 никак по-другому не положишь — только в виде решётки с одним пропуском? Нарисую-ка эту решётку. Радиус апельсина возьму за 1.
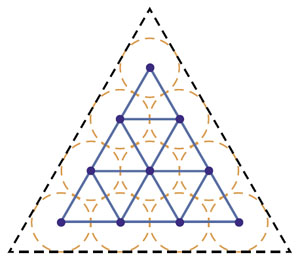
Рис. 7
Квантик изобразил апельсины кругами на плоскости — задача ведь фактически сводилась к этому плоскому варианту. У него получился большой треугольник, разделённый на меньшие, а блюдо и апельсины Квантик нарисовал пунктиром (рис. 7).
— Центры апельсинов отстоят от края блюда хотя бы на 1 и поэтому лежат в пределах треугольной решётки. Стороны маленьких треугольников равны 2. Тогда для центров такая задача получается:
Треугольник со стороной 6 разбит на маленькие треугольники со стороной 2 (рис. 7). В нём лежат 9 точек, расстояния между любыми двумя точками не меньше 2. Доказать, что все точки лежат в вершинах маленьких треугольников (в узлах решётки).
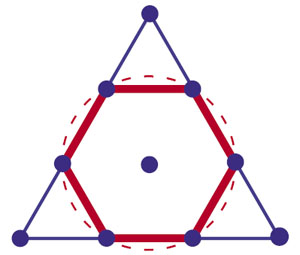
Рис. 8
— Что-то тут напоминает котлетную теорему... Ага, если откинуть три угла, остаётся шестиугольник — та же «ромашка»! Нарисую-ка его красным цветом (рис. 8). Можно даже вокруг него невидимый круг описать радиуса 2. Но дальше-то что? У нас же теперь 9 точек, а не 6. Стоп! А что если 6 точек из 9 попадают в красный шестиугольник? Вторая котлетная теорема! Ведь 6 точек лежат тогда в невидимом круге, а значит, либо одна точка в центре и 5 — на краю круга, либо все 6 точек на краю. Но край круга пересекается с шестиугольником только в его вершинах! Значит, если 6 точек внутри шестиугольника — они все в узлах решётки.
Квантик перевёл дух и продолжил разбираться.

— А сколько точек может быть снаружи шестиугольника, то есть в трёх «угловых» треугольниках? Ага, в каждом максимум по три, то есть всего трижды три — девять? Нет, я неправильно считаю. Ведь если точка на красной стороне углового треугольника, то она и в шестиугольнике тоже. А мне надо понять, сколько точек могут быть строго вне шестиугольника. В каждом угловом треугольнике такая точка... одна! Значит, вне шестиугольника — максимум 3 точки, а в шестиугольнике — минимум 6. Ура!!! Ведь тогда эти 6 (или больше) точек лежат в узлах решётки. И в каждый угловой треугольник попадёт хоть одна из них, поэтому и в угловых треугольниках точкам некуда деваться кроме узлов. Всё доказано!
Квантик захотел узнать, не встречались ли раньше подобные задачи. Полазив по интернету, он выяснил, что автор задачи про блины — А. М. Абрамов, про загнутый прямоугольник — В. В. Произволов, про апельсины — Н. П. Долбилин, который, кстати, предлагал подумать над общим случаем — когда в блюде помещается не 10, а 15 апельсинов, 21 и т.д. (в виде треугольной решётки, но с большим количеством точек). Задача про котлеты оказалась глубоким фольклором — наверняка каждый математик, занимавшийся проблемой упаковки кругов в круге, её знал (а «официальное» доказательство опубликовал в 1968 году Рональд Грэхем).
А ещё Квантик нашёл задачу М. А. Евдокимова из Турнира городов, которая очень ему понравилась:
Апельсины в кубе
В кубическую коробку поместили 3 одинаковых апельсина. Докажите, что в такую же пустую коробку можно поместить 4 таких же апельсина.
Квантик справился с ней за пару часов и решил рассказать доказательство в журнале «Квант» — уж больно оно непростое получилось, хотя и короткое.
А нашим читателям он решил напомнить ещё несколько «кулинарных» задач, уже встречавшихся на страницах нашего журнала. Справитесь?
Печенья на противне
На прямоугольный противень помещается 100 круглых печений. Обязательно ли на такой же противень можно уложить 400 круглых печений в два раза меньшего радиуса?
Торт с глазурью
Квадратный торт облит сверху и по бокам глазурью. Разрежьте его на 5 цельных кусков, в которых поровну и торта, и глазури.
Рис. 9
Лишний апельсин
В плоской коробке в один слой вплотную лежат одинаковые круглые апельсины — 8 рядов по 5 штук в каждом (рис. 9). Удастся ли поместить в коробку ещё один такой апельсин?
Художник Мария Усеинова


















Рис. 1