Парадокс «Последней ручки»

Амелия Алаева
«Квантик» №3, 2020

Да уж, восьмой класс — это вам не седьмой! На дом теперь Маше задавали очень много. Да и в школе на уроках писанины не убавилось. Всё время что-то пишешь. У Маши даже мозоль на среднем пальце появилась. Да что там — мозоль! Расход ручек вырос! И это ещё повезло, если в ручке закончился гель. Чаще ручка банально теряется, ломается. Иногда ручку просит соседка по парте Таня. Она, безусловно, хорошая подруга, но обладает уникальной способностью регулярно забывать ручки дома. И она ещё ни разу ни одну из них не вернула. Это не беда — Маша даёт ей свою ручку, а из пенала берёт новую. Ведь она не только любознательная, но и запасливая.

Маша подсчитала, что в среднем ручка служит семь дней, а поскольку в первой четверти 40 учебных дней, то на четверть ей нужно примерно шесть ручек. К началу учебного года у неё было как раз шесть ручек — целая упаковка. И всё бы хорошо, но вот уже первый день второй четверти, а на каникулах Маша была так занята, что забыла купить ручки. А тут как раз сочинение на тему «Как я провела осенние каникулы». Страшно подумать, что случится, если закончится та самая шестая ручка. Но ручка выдержала. Маша облегчённо вздохнула и поклялась страшной клятвой, что по дороге из школы зайдёт за новой пачкой ручек. Но, ясное дело, не зашла, потому что... ну мало ли почему. И на следующий день ручка снова не кончилась, но Маша уже не на шутку волновалась и ругала себя ужасными словами за разгильдяйство. Невозможно представить, что Маше придётся просить у кого-то ручку. Это ей-то, Маше, которая славится пунктуальностью и нескончаемым запасом ручек. Ей, Маше, которая всегда готова снисходительно выдать ручку в вечное пользование всем растяпам, неужели ей самой придётся попрошайничать, как Тане? Этот позор Маша не пережила бы. И надо ж такому случиться, что и во вторник Маша не смогла зайти в магазин (мало ли почему). А в среду контрольная по геометрии на повторение, а ручка может подвести в любой момент. Маша боялась дышать и пыталась изъясняться лаконично. От этого строчка, которая в нормальных условиях выглядела бы так: «Следовательно, данные прямоугольные треугольники равны по катету и гипотенузе», приобрела удивительный вид: «С-но, д-е пр. тр-ки = по к. и г.».

Ручка выдержала. Она потом писала ещё весь урок русского, где учительница вдруг вздумала устроить внезапный диктант. По дороге домой Маша, наконец, купила десяток ручек и вздохнула с облегчением, но задумалась: «Интересно, а сколько ещё продержится героическая ручка? Тане я не дам её ни за что!». Ручка прослужила ещё целый четверг и половину пятницы. Только на предпоследнем уроке — это была история — Маше пришлось взять новую. Вот это да! 10 дней напряжённейшей работы. «Суперручка», — уважительно подумала Маша и выбросила её в мусорную корзину у выхода из кабинета.

В начале третьей четверти повторилась примерно та же история: ручки, которой Маша начала писать ещё в декабре, хватило на дольше, чем обычно.

Как-то вечером, когда Маша делала уроки, раздался звонок в дверь. На пороге стоял смущённый сосед Иван Петрович.

— Э-э-э... Добрый вечер, Маша. Мне очень неудобно, но не найдётся ли у тебя запасной ручки? А то моя кончилась. Совсем внезапно. Я завтра отдам.

Маша была польщена до глубины души. Конечно, она подарила Ивану Петровичу самую лучшую ручку. Ещё она спросила, не нужна ли ему случайно линейка или транспортир, и, разумеется, не удержалась и рассказала историю о суперручках.

— Ого, да ты теперь настоящий эксперт по ручкам! И, кажется, столкнулась с очередным парадоксом теории вероятностей! — пришёл к заключению Иван Петрович, который хорошо понимал проблему, потому что работал математиком в университете. А когда работаешь математиком в университете, особенно чётко понимаешь, как быстро заканчиваются ручки.

— Да как же так! Я постоянно нахожу новые парадоксы, похоже, это уже традиция. Что за математическая загадка на этот раз?

— Твой способ вычисления среднего времени службы ручки абсолютно верный, он годится для всех ручек. Но вот для последней ручки он не годится. То есть и для последней тоже годится. Но для последней ручки, если четверть уже кончилась, — не годится. Хотя эта ручка ничем не отличается от предыдущих. Правда, не совсем. Всё же отличается: те ручки кончились раньше, чем кончилась четверть, а эта — позже. И у неё средний срок службы немного больше, чем у предыдущих.

Маша опасливо попятилась:

— Иван Петрович, родненький, вы в здравом уме и твёрдой памяти утверждаете, что если четверть не кончилась, то у ручки один средний срок службы, а если кончилась, то другой? То есть ручка знает, что четверть кончилась, и поэтому она...

— Именно это я и хочу сказать, мой юный друг, кроме того, что ручка знает, что четверть кончилась. Хотя, если бы она не кончилась, то, наверно, ручка не кончилась бы раньше, чем она кончилась. Но она не кончилась раньше, чем кончилась четверть, а поэтому кончилась позже!

— Профессор, но это же бред!

— Это кажущийся бред. Иными словами — парадокс, а именно — Inspection Paradox. Подсчитав среднее время службы ручек, ты примерно знаешь, когда кончится ручка. И тут кончается не ручка, а четверть. При этом оказывается, что ожидаемое время работы ручки зависит от того, кончилась четверть или нет, пока ты пишешь этой ручкой. Эта зависимость приводит к тому, что ожидаемый срок службы этой ручки несколько больше, чем у остальных ручек.

— Что-то не очень понятно, как ожидаемый срок службы последней ручки зависит от конца четверти.

— Приведу простой пример. Предположим, у нас есть монета, которую мы подбрасываем до тех пор, пока не выпадет орёл. Математическое ожидание числа орлов при каждом отдельном броске равняется 0,5. Но наш эксперимент закончится, только когда выпадет орёл, поэтому математическое ожидание числа орлов при последнем броске всегда равно 1, а не 0,5.

— Ясное дело. Ведь мы бросаем, пока не выпадет орёл. Значит, в последний раз обязательно будет орёл, или наоборот — как выпал орёл, значит, это был последний бросок.

— А теперь представь себе игральный кубик. В среднем на нём выпадает 3,5 очка при каждом броске. Будем бросать этот кубик до тех пор, пока сумма очков, выпавших при всех бросках, не достигнет... э... скажем, 100. Вот сумма стала 100 или больше, всё — уже не бросаем. Скажи, на каком броске более вероятно, что сумма преодолеет 100? На броске, когда выпала единица, или на броске, когда выпала шестёрка?

— Чем больше выпало, тем сильнее увеличивается сумма, тем более вероятно, что она перескочит 100.

— Совершенно верно. Значит, более вероятно, что сумма 100 наступит при броске, давшем 6 или 5 очков, чем при броске, когда выпало 1 или 2 очка. Поэтому математическое ожидание числа очков при последнем броске больше, чем 3,5.

Кубиков игральных у меня под рукой нет. Давай проведём этот эксперимент на компьютере. Нам понадобится ГСЧ — генератор случайных чисел. Надеюсь, ты не забыла, что это такое¹. Пусть ГСЧ даёт случайные числа от 1 до 6, мы будем их складывать до тех пор, пока их сумма не станет равна 100 или больше. Повторим это много раз.

Профессор был мастером на все руки. Он не только превосходно знал математику, но и умел программировать. Иван Петрович включил компьютер и быстро написал программу, которая «бросает» игральный кубик до тех пор, пока сумма очков не окажется 100 или больше. Причём делает это много раз. Маша с волнением нажала «Запуск» и даже удивилась, когда программа выдала диаграмму распределения вероятностей последних слагаемых².

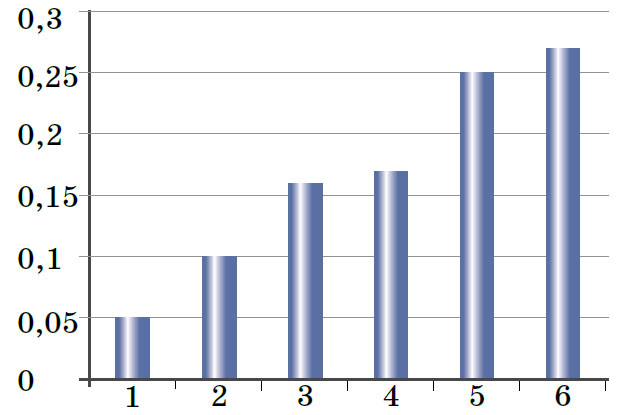
— Посмотри, насколько чаще при последнем броске выпадает пятёрка или шестёрка, чем единица или двойка, — довольным тоном сказал Иван Петрович, любуясь диаграммой. — Знаешь, какое у нас среднее?

— Да уж точно не три с половиной.

— А среднее у нас... Вот: примерно 4,28! Маша, обрати внимание: если бы мы просто бросали игральный кубик 100 или 200 раз, то парадокс себя бы не проявил. Важно, что условие остановки — достигнутая сумма.

— Классно, Иван Петрович. Просто слов нет, какой это классный парадокс. Но ручки-то здесь причём?

— И с ручками примерно то же самое. Что более вероятно: что четверть кончится на ручке, которая мало пишет, или что на той, которая долго пишет?

— Долгопишущая ручка пишет долго, малопишущая — мало. Поэтому более вероятно, что конец четверти придётся на срок службы долгопишущей ручки.

— Вот-вот, именно так. Поэтому ручки, на которые пришёлся конец четверти, пишут в среднем дольше, чем те, которые были в начале четверти.

— Да уж. Необычный парадокс... Зато теперь я могу не волноваться, если я забыла вовремя купить ручки, по крайней мере ещё пару дней... — облегчённо вздохнула Маша, которая всегда найдёт повод для волнения. — Кстати, как вы там его назвали, этот парадокс? Ин... инт... инп-что?

— По-английски его называют Inspection Paradox.

— А почему? При чём тут инспекция?

— Впервые на него обратили внимание американские военные, когда занимались обслуживанием, то есть инспекцией радиолокационных станций. До истечения заявленного срока службы локатор ремонтируют, а как срок вышел — заменяют при первой же поломке. Вот и выяснилось, что очень часто последнюю поломку приходится ждать дольше, чем предыдущие. Инспектор ждёт-ждёт, а всё никак.

— Ага, как и я ждала-ждала, пока ручка кончится. А по-русски как называется? Давайте назовём его «Парадокс конца четверти». Или лучше «Парадокс последней ручки». Или... Завтра расскажу обо всём Тане. — А про себя Маша подумала, может всё-таки удастся её перевоспитать, чтобы она не забывала ручки?

Художник Мария Усеинова

¹ Подробнее о генераторе случайных чисел (ГСЧ) см. статью «Парадокс двух конвертов» (см. «Квантик» № 8 за 2016 год).

² Вы можете запустить эту программу по адресу kvan.tk/lastpen.