Неопределенность — основа квантовой физики

Андрей Варламов, Жак Виллен, Аттилио Ригамонти
«Квант» №1, 2021

1900 год, знаменующий начало XX века, является еще и датой возникновения квантовой механики. Именно тогда Макс Планк нашел окончательное решение задачи о тепловом излучении тел, поставленной Густавом Кирхгофом четырьмя десятилетиями ранее. Решение Планка основывалось на предположении, что энергия физической системы квантуется. Например, если монохроматический свет частотой ν заключен в зеркальной камере, то его энергия обязательно окажется кратной одному «кванту» энергии, равному hν, где h = 6,63 · 10⁻³⁴ Дж ∙ с — постоянная величина, называемая теперь постоянной Планка. Сначала эта гипотеза казалась относительно невинной Однако спустя тридцать лет выяснилось, что она бросает вызов детерминистическому пониманию физики...

Принцип неопределенности

Вернер Гейзенберг (слева) и Нильс Бор (справа) — ученые, открывшие квантовый индетерминизм

В 1927 году немецкий физик Вернер Гейзенберг (1901-1976) сформулировал следующий принцип, называемый принципом неопределенности. Рассмотрим частицу массой m, которая движется по оси х со скоростью v. Если нам удастся измерить ее скорость с точностью Δv, то ее положение x оказывается невозможным определить с точностью Δх более высокой, чем ħ/(mΔv), где ħ = h/(2π). (Постоянную ħ также называют постоянной Планка.) Иными словами, тΔхΔи ≥ ħ. Это утверждение можно распространить и на движение частицы, перемещающейся в трехмерном пространстве. Вместо того чтобы рассуждать о ее скорости \(\overrightarrow{v}\), часто вводят импульс \(\overrightarrow{p}=m\overrightarrow{v}\). В этом случае соотношение неопределенности в проекции на ось x записывают следующим образом:

ΔхΔp_x ≥ ħ. (1)

Аналогично оно записывается и для двух других составляющих вектора импульса и координат. Это неравенство удивительно. Законы Ньютона позволяют, исходя из начальных условий, очень точно определить положение и скорость объекта в любой момент времени. В физике Ньютона, так называемой классической механике, нет места для неопределенности. Но этот детерминизм, свойственный макроскопическому миру, перестает действовать в атомном масштабе. Объясним, почему это происходит.

Для начала приведем иллюстрацию соотношений неопределенности. Направим поток частиц (например, электронов или нейтронов) на стенку, в которой есть отверстие диаметром Δх (рис. 1). Некоторые из них пролетят через отверстие. В момент прохождения отверстия их положение определяется в плоскости стенки с точностью Δх. При этом параллельные этой плоскости составляющие их скорости могут быть известны только с некоторой неопределенностью, обратно пропорциональной Δх. Даже если скорость какой- то частицы при подлете строго перпендикулярна стенке, то после прохода через отверстие скорости всех прошедших частиц распределятся внутри некоторого телесного угла. Таким образом, здесь мы сталкиваемся с тем же явлением дифракции, что и в случае световых лучей, проходящих через узкую щель.

Рис. 1. Если частица проходит через отверстие или щель ширины Δх, то ее положение в направлении x известно с точностью Δх, а ее импульс в этом направлении может быть известен только с некоторой точностью Δp_x. Если частица является частью пучка с импульсом p_z вдоль оси z, то прохождение пучка через щель вызывает его расхождение под углом, определяемым отношением Δp_x/p_z

Неопределенность и измерение

Согласно толкованию Гейзенберга, квантовый индетерминизм является результатом взаимодействия наблюдаемой частицы с измерительным прибором. Вот как он рассуждал.

Предположим, мы хотим проанализировать движение электрона. Как это сделать? Невооруженный глаз, очевидно, не обладает достаточным разрешением, а что насчет микроскопа? Разрешение микроскопа определяется диапазоном длин волн X наблюдаемого излучения. Для света они составляют порядка 100 нм (т. е. 100 миллиардных частей метра), частицы меньшего размера не будут видны. Поэтому с помощью микроскопа невозможно увидеть атомы, размер которых порядка 0,1 нм, и тем более — обнаружить электроны. Представим, однако, что нам удалось сделать микроскоп с использованием электромагнитного излучения более короткой длины волны: рентгеновского или даже γ-излучения, длина волны которого составляет менее 0,01 нм. Стало бы такое изобретение идеальным инструментом для точного измерения положения и скорости электрона?

Прежде чем праздновать победу, пристальнее рассмотрим наш воображаемый опыт. Для того чтобы получить информацию о положении электрона, необходимо использовать как минимум один квант электромагнитного излучения. Энергия E такого кванта равна hc/λ, где c — скорость света в вакууме. Чем короче длина волны, тем большую энергию несет квант. Однако импульс кванта пропорционален этой энергии, а при столкновении с электроном квант неизбежно передает ему часть своего импульса. По этой причине любое измерение положения, тем более для рентгеновского или γ-излучения, вносит неопределенность в величину импульса электрона. Точный анализ процесса показывает, что произведение неопределенностей в установлении положения электрона и измерении его импульса не может быть меньше постоянной Планка. Это возвращает нас к принципу Гейзенберга.

Можно предположить, что такое рассуждение относится только к конкретному случаю или что метод измерения неверен. Ничего подобного. Самые выдающиеся ученые (в частности, как будет рассказано далее, Альберт Эйнштейн) пытались придумать мысленные эксперименты, которые могли бы позволить определить положение и импульс тела с большей точностью, чем предписано соотношениями неопределенности. Ни одна из этих попыток успехом не увенчалась. Принцип неопределенности — это закон природы, фундаментальный закон. Не следует думать, что эта неопределенность всегда связана с погрешностями измерения: многочисленные экспериментально установленные факты показывают, что она имеет фундаментальную природу и что соотношение неопределенности соблюдается даже при использовании самых точных измерительных устройств.

Детерминированный и квантовый миры

Кажется, что принцип неопределенности противоречит тому, что мы знаем об окружающем мире. До какой степени он опровергает наши детерминистические представления? Для объекта массой m принцип Гейзенберга выглядит как ΔxΔv_x ≥ ħ/m. В случае шара массой 0,7 кг для игры в петанк (провансальский национальный вид спорта, бросание шаров) предел произведения ΔxΔv_x немного превышает 10⁻³⁴ м²/с, что очень близко к нулю. Если положение шара известно с высокой точностью, например Δx = 10⁻¹⁰ м (близко к размеру атома!), то минимальная неопределенность Δv_x для скорости остается крайне низкой — от 0,03 нанометра в час. Поэтому макроскопический мир, сообразно нашим представлениям, несмотря на соотношение Гейзенберга, остается практически детерминистическим.

А с какого же размера квантовые эффекты становятся существенными? Пойдем дальше по направлению к наномиру и обсудим броуновское движение мельчайших частиц в жидкости. Рассмотрим броуновскую частицу массой около 10 кг и диаметром примерно 1 мкм. Соотношение неопределенности говорит нам, что произведение ΔxΔv_x должно превышать величину ħ/m, в рассматриваемом случае составляющую примерно 10⁻²¹ м²/с. Если мы хотим знать положение броуновской частицы с точностью до 1% от ее размера, то неопределенность в измерении ее скорости не может превышать 10⁻¹³ м/с, что по-прежнему очень мало. В самом деле, скорость движения броуновской частицы составляет примерно 10⁻⁶ м/с, что превышает найденную погрешность Δv_x более чем в миллион раз! Это означает, что даже мелкие частицы броуновского движения правильно описаны классической механикой. Таким образом, соотношение неопределенности становится существенным только для частиц, значительно меньших броуновской. Так, оно становится крайне важным для электрона. Важным настолько, что, как будет показано далее, на его основании оказывается возможным оценить размер атома.

От принципа неопределенности к радиусу атома. Рассмотрим атом самого простого элемента — водорода, который состоит из протона и электрона. Первое по существу верное описание атома водорода привел британский физик Эрнест Резерфорд (1871-1937). Он выяснил, что электрон, обладающий отрицательным зарядом −e, и протон, несущий заряд такой же по величине, но противоположный по знаку, удерживаются вместе благодаря электростатическому взаимодействию. При этом электрон вращается вокруг протона, подобно тому как Земля вращается вокруг Солнца. Заметим, что в таком описании вращающийся электрон представляет собой циркулярный электрический ток. Однако любой замкнутый контур, по которому проходит ток, подобно антенне испускает электромагнитное излучение. В результате, согласно описанию Резерфорда, электрон должен был бы терять энергию... и в конечном итоге «упасть» на протон (рис. 2)! Но мы знаем, что он не падает — атом водорода стабилен. Чтобы дать объяснение этому факту, необходимо было ввести некий новый физический принцип, который выходил бы за рамки ньютоновской физики. Им стал принцип неопределенности Гейзенберга. В соответствии с этим принципом, бедный электрон должен вращаться в области пространства некоторого размера с плохо определенной, но не равной нулю скоростью. И из этих смутных соображений мы собираемся оценить размер атома!

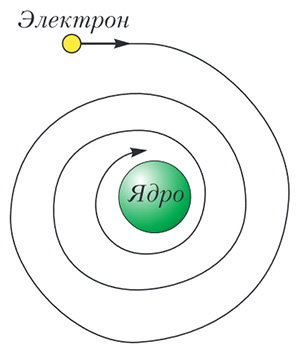
Рис. 2. В классической физике атом Резерфорда был бы нестабилен: электрон в конце концов упал бы на ядро

Пусть v и 2R суть скорость электрона и диаметр сферы, в пределах которой он движется. Согласно формуле (1), 2mRv > ħ. Следовательно, кинетическая энергия электрона, равная mv²/2, не может быть меньше чем ħ²/(8mR²). Добавляя электростатическую энергию его взаимодействия с протоном, находим неравенство для полной энергии электрона W:

\(W\geqslant \frac{-e^2}{2\pi \varepsilon _{0}R}+\frac{\hbar}{8mR^2}\). (2)

где элементарный электрический заряд e равен 1,6 ∙ 10⁻¹⁹ Кл, а ε₀ — электрическая постоянная, равная 8,85 ∙ 10⁻¹² Ф/м.

Энергия W атома не может стать ниже минимума этого выражения, который, как легко понять, реализуется при R = R₀, где

\(R_0=\frac{4\pi \varepsilon _0\hbar^2}{me^2}\approx 0,0529\) нм. (3)

Равновесное состояние механической системы соответствует минимуму ее потенциальной энергии. Радиус атома R не может сильно превышать величину R₀, потому что потенциальная энергия электрона при этом была бы слишком высока, но он не может быть и намного меньше R₀, потому что тогда кинетическая энергия была бы слишком велика, а полная энергия должна сохраняться. Именно поэтому электрон и не падает на ядро! Выражение (3) дает нам представление о размере атома водорода — это примерно 1 ангстрем (десятая часть нанометра).

Спектр излучения атомов — ключ к атомной структуре. Пребывая в своем основном состоянии (минимума полной энергии), атом терять энергию не может. Однако он может ее получать, переходя при этом в то или иное «возбужденное» состояние. Причем бесконечно долго возбужденным он не остается — через некоторое время, излучая свет, атом возвращается в свое основное состояние. Этот свет соответствует излучению точно определенных частот, т. е. спектр излучения атома является «линейчатым». Частоты спектральных линий образуют так называемое дискретное множество, т. е. их можно пронумеровать, например в зависимости от интенсивности каждой из них. Чтобы объяснить происхождение такого линейчатого спектра, разумно предположить, что значения, которые может принимать энергия данного атома, также составляют дискретное множество. Поскольку свет может излучаться только в виде фотонов, то закон сохранения энергии требует, чтобы энергия hν каждого фотона была равна разности между двумя допустимыми значениями энергии атома (рис. 3). Таким образом дискретный вид спектра излучения объясняется, по крайней мере, качественно. Ос тается выяснить, почему значения энергии атома составляют дискретное множество.

Рис. 3. Энергетическая диаграмма атома водорода. Атом переходит из основного состояния в возбужденное путем поглощения фотона, энергия которого соответствует разнице между двумя энергетическими уровнями атома

В начале XX века вопрос о природе атома — мельчайшей частицы вещества, являющейся носителем его свойств, был одним из центральных в физике. Предлагаемые модели, будучи внутренне противоречивыми или не соответствующими эксперименту, одна за другой опровергались. И вот в 1913 году датский физик Нильс Бор (1885-1962) предложил математически простую теорию атома, объясняющую существующие экспериментальные данные, однако основанную на столь необычных допущениях, что он сам назвал их «постулатами».

Атом по Нильсу Бору

Нильс Бор, предлагая свою модель атома, ничего не знал о принципе неопределенности, до открытия которого оставалось еще 14 лет.

В модели Бора, как и в модели Резерфорда, электрон вращается вокруг ядра, подобно тому как Земля вращается вокруг Солнца, однако при этом электрон может двигаться только по определенным орбитам. Например, круговые орбиты возможны только в том случае, когда произведение импульса mv электрона на радиус его орбиты R, это произведение называют «моментом импульса», является кратным постоянной Планка:

mvR = ħn. (4)

Однако импульс электрона и радиус орбиты связаны также и тем обстоятельством, что центростремительное ускорение электрона, равное v²/R, обеспечивает сила электростатического притяжения. Для атома водорода, ядро которого состоит из протона, последняя равна −е/(4πε₀R). Отсюда уже можно найти радиусы R_n−1 разрешенных орбит для каждого значения n. Так, для n = 1 находим уже знакомое нам значение R₀, которое соответствует основному состоянию. Предоставим читателю самому вывести общую формулу, применимую к возбужденным состояниям электрона.

Модель Бора, разработанная в 1913 году, довольно хорошо описывала спектры излучения атомов (рис. 4), однако вскоре выявились и ее недостатки. Спустя десятилетие теория Бора была концептуально расширена введением вероятностного описания нахождения электрона. Так, оказалось, что значение R₀ (расстояние от электрона до ядра) в атоме водорода может считаться лишь некоей усредненной величиной; принцип неопределенности не позволяет четко определить расстояние между протоном и электроном.

Рис. 4. Модель Бора позволяет объяснить спектр излучения атома водорода в видимой области. Линии, расположенные вблизи длин волн в 410, 434, 486 и 656 нм, соответствуют переходам на уровень n = 2 из возбужденных состояний n = 6, 5, 4 и 3

Вероятность нахождения. Предположим, что в какой-то момент нам удалось установить положение электрона. Можно ли предсказать его положение через секунду? Нет, поскольку знание положения электрона неизбежно привело бы к полной неопределенности его скорости. Ни один прибор, ни одна теория не смогли бы предсказать, куда направится электрон. Так что же делать?

Сменим стратегию и отметим точку пространства, в которой обнаружен электрон, затем еще одну точку — результат аналогичного измерения с другим электроном и многократно повторим эту процедуру. Хоть и невозможно предсказать, где появится следующая отметка, все же их распределение следует некоему правилу. Плотность отметок, которая варьирует в зависимости от точки пространства, указывает на вероятность нахождения электрона во время измерения. Мы были вынуждены отказаться от описания движения электрона, но можем теперь определить вероятность его нахождения в каждой точке пространства. Поведение электрона в наномире характеризуется вероятностью!

Читатель, не знакомый с этой концепцией, не может оценить роль случайности в законах природы. Тем не менее, как вы увидите, такая вероятностная теория подтверждается серьезными экспериментальными доказательствами.

Таким образом, в наномире нахождение электрона определяется законами вероятности. Расставленные нами отметки в совокупности напоминают облако, так же как капельки воды образуют в небе облака различной плотности. Такое «электронное облако» является более точным представлением об электроне, чем маленькая планета, вращающаяся вокруг ядра, как его изображал Резерфорд.

Волна де Бройля и уравнение Шрёдингера

Что же определяет структуру электронных облаков? Существует ли уравнение, которое описывает квантовую механику так же, как классическую механику описывают законы Ньютона? Да, такое уравнение существует. Оно было предложено в 1925 году австрийским физиком Эрвином Шрёдингером (1887-1961) и является основой атомной физики и теоретической химии.

Теория Шрёдингера обобщила предложенную годом ранее французом Луи де Бройлем (1892-1987) революционную идею, которая состояла в том, что с любой частицей, обладающей импульсом p, можно связать волну длиной λ = h/p. Таким образом, любая частица может проявлять как корпускулярное поведение, так и волновое, как это делает свет. Подобно предложенной Джеймсом Максвеллом (1831-1879) волновой теории света, где электрическое поле E (x, y, z, t) является функцией времени и трех пространственных координат, уравнение Шрёдингера описывает состояние частицы с помощью «волновой функции» ψ (x, y, z, t), квадрат модуля которой определяет плотность вероятности нахождения частицы в заданный момент времени t в точке (x, y, z). Этот подход был основан на аналогии с оптикой, где квадрат модуля электрического поля определяет вероятность нахождения фотона в данной точке. Различие же заключается в том, что электрическое поле является физически измеримым, например по его действию на электрически заряженные объекты, тогда как введенная де Бройлем волновая функция ясного физического смысла не имела.

С помощью уравнения Шрёдингера оказалось возможным найти пространственное распределение плотности вероятности электрона для его возможных состояний в атоме водорода. Изобразив эти распределения плотности вероятности на плоскости разными цветами, получают изображение различных атомных орбиталей (областей, в которых вероятность нахождения электрона наиболее высока). Такие изображения заменяют электронные орбиты модели атома Бора и наглядно представляют поведение электронов в атоме. Основанные на уравнении Шрёдингера расчеты объясняют существование дискретных уровней энергии, которые и являются причиной линейчатых спектров, наблюдаемых при излучении и поглощении света. Подобные, но более сложные вычисления позволяют понять, как между атомами образуются химические связи.

Заметим, что работы де Бройля и Шрёдингера предшествовали открытию Гейзенбергом принципа неопределенности. Последний прост, краток, элегантен, однако содержит меньше информации, чем уравнение Шрёдингера.

Опыт Дэвиссона—Джермера. Предложенная де Бройлем концепция связи между волнами и частицами, так называемый корпускулярно-волновой дуализм, привела к идее применения оптических методов исследования с заменой света на потоки частиц. Так, в 1927 году американские физики Клинтон Дэвиссон и Лестер Джермер бомбардировали электронами кристалл никеля. В результате они получили дифрактограммы, подобные возникающим при облучении кристаллов рентгеновскими лучами. Для интерпретации полученных дифракционных картин электронам следовало приписать определенную длину волны, и она совпадала с величиной, предсказанной де Бройлем. Таким образом, эксперимент блестяще подтвердил его гипотезу.

Исследование твердых тел с помощью дифрактометрии. Дифракция электронов редко используется для изучения кристаллов, потому что электроны поглощаются материей куда сильнее, чем рентгеновские лучи. Гораздо больший интерес представляет собой еще одна элементарная частица — нейтрон. Если речь идет о наблюдении легких атомов или изучении атомных магнитных свойств, то дифракция нейтронов оказывается предпочтительнее рентгеновских лучей. Последняя позволяет составлять карты электронной плотности, в то время как поляризованные нейтроны дают возможность исследовать не все, а лишь электроны, находящиеся на внешних оболочках атома, именно те, которые определяют его химические и магнитные свойства. Недостатком этого метода является то, что для производства нейтронов требуются дорогие и громоздкие ядерные реакторы, в то время как рентгеновской установкой легко оснастить даже скромную лабораторию.

Нулевые колебания атомов

Принцип неопределенности позволяет получить интересную информацию о движении атомов в твердых телах. Под твердыми телами здесь мы будем подразумевать кристаллы, поскольку при низких температурах кристаллическая структура является устойчивой формой существования почти всех чистых веществ. Атомы в кристалле не являются неподвижными: они колеблются вокруг положения равновесия. Амплитуда этих колебаний очень мала: расстояние между двумя соседними атомами всегда остается близким к своему среднему значению, которое составляет около нескольких десятых нанометра. Как правило, эти колебания обусловлены тепловым движением: чем температура выше, тем больше амплитуда колебаний. Что же происходит, когда температура опускается до абсолютного нуля (0 К, т. е. −273,15 °C)? Можно предположить, что колебания прекращаются и атомы замирают. Однако в этом случае их положение было бы точно фиксировано, в то время как скорость была бы равна нулю, т. е.

Δx = Δp = 0, что нарушило бы соотношение неопределенности. Отсюда следует, что движение атомов прекратиться не может даже при абсолютном нуле температур: в этом случае тепловые колебания сменяются на «нулевые колебания».

Попробуем разобраться в этом подробнее на примере простого кристалла, состоящего из атомов лишь одного сорта ( например, водорода, кислорода, железа). Упрощенное, но качественно приемлемое описание движения атома в кристалле относительно его соседей можно получить, предполагая, что при отклонении от положения равновесия на него действует возвращающая сила, пропорциональная расстоянию, как если бы его удерживала пружина. В таком случае движение атома относительно положения равновесия описывается формулой x(t) = x₀cos (ωt − α), где x₀ — максимальная амплитуда колебаний (для двух других координат формулы аналогичны). При этом скорость атома равна v_x(t) = −ωsin(ωt − α). Соотношение неопределенности требует, чтобы ΔxΔv ≥ ħ/m и, следовательно, ωx₀² было не менее ħ/m, где m — масса атома. Частота ω для большинства веществ лежит в диапазоне между 10¹³ и 10¹⁴ Гц (характерную частоту колебаний атома в твердых телах называют частотой Дебая). Заменяя массу m на Am_н, где A — массовое число, а m_H — средняя масса нуклона, около 1,67 ∙ 10⁻²⁷ кг, получим, что х₀ в метрах должна составлять не менее 10⁻¹¹/\(\sqrt{A}\). Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.

Сомнения могут оставаться только для наименьших значений A, т. е. для водорода (A = 1) и гелия (A = 4). Оказывается, что только гелий является исключением из правила: если давление не превышает 2,5 МПа, то нулевые колебания действительно делают его кристаллическое состояние неустойчивым при любых температурах. Все остальные простые тела, включая водород H₂ , при приближении температуры к абсолютному нулю рано или поздно затвердевают при любом давлении.

Квантование магнитного момента. Мы уже видели, что согласно квантовой механике ни в какой момент времени невозможно установить точные значения положения \(\overrightarrow{r}\) и скорости \(\overrightarrow{v}\) электрона, вращающегося вокруг ядра. Еще более необычными оказываются свойства его магнитного момента.

Магнитный момент — это векторная величина, характеризующая свойство определенных объектов ориентироваться в магнитном поле. Например, стрелка компаса располагается по магнитному полю Земли, указывая направление на северный магнитный полюс. Многие из элементарных частиц и объектов атомного масштаба также обладают магнитным моментом: электрон, нейтрон, протон, а также большая часть ядер, атомов и ионов. Пространственные составляющие магнитного момента обозначаются μ_х, μ_у, μ_z.

Когда стрелка компаса сориентирована в определенном направлении, то четко определены и все три составляющие ее магнитного момента. В отличие от компаса, электрон или нейтрон являются объектами, принадлежащими к квантовому миру. Для них может быть измерена только одна из трех составляющих магнитного момента, при этом она способна принимать только два противоположных значения: −μ или +μ. Это, казалось бы, парадоксальное утверждение было подтверждено экспериментально: первыми опытные данные, говорящие в пользу квантования магнитного момента представителей квантового мира, еще в 1922 году получили Отто Штерн и Вальтер Герлах. В своих экспериментах они направляли пучок атомов серебра, которые благодаря электронам внешней оболочки обладают магнитным моментом, сквозь неоднородное магнитное поле. В результате было обнаружено, что этот пучок разделяется строго пополам, что и доказывает квантование магнитного момента всего на два дискретных значения (рис. 5). Действительно, если бы магнитный мо мент мог принимать хотя бы три значения, то пучок делился бы натрое, а если бы магнитный момент атомов серебра мог меняться непрерывно, то пучок просто расходился бы в конус.

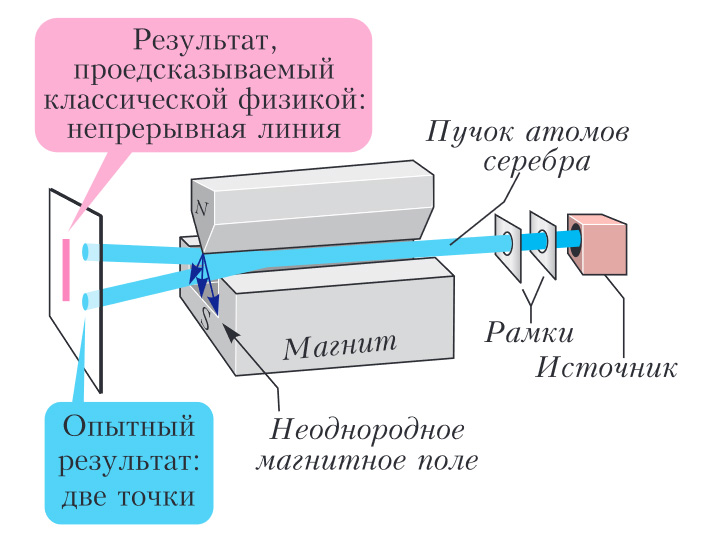
Рис. 5. Принцип опыта Штерна—Герлаха. Атомы серебра проходят через вертикально направленное неоднородное магнитное поле. Согласно классической физике, пучок частиц с непрерывным распределением магнитного момента должен расходиться конусом. Опыт же показывает, что он делится на две компоненты

Еще несколько слов о пучке атомов серебра. Выберем ось x вдоль направления магнитного поля. Тогда существует такое состояние атома серебра, в котором μ_х = −μ, и другое, в котором μ_x = +μ. Существует также состояние, при котором μ_y = μ. Что произойдет, если частица находится в этом состоянии и измеряется компонента μ_х? Измерение с равной вероятностью даст μ_х = −μ или μ_х = +μ. Таким образом, среднее значение всех измерений μ_х, которые можно произвести в состоянии μ_у = μ, равно нулю. То же самое относится к среднему значению всех измерений μ_х в состоянии μ_у = −μ. Чтобы принять в расчет эти свойства, в квантовой механике считается, что состояние μ у = μ является «соединением» состояний μ_х = −μ и μ_х = +μ.

Кот Шрёдингера. Концепция «смешения состояний» очень хорошо описывает реальность в масштабе атомного мира. Интересно попробовать распространить ее действие на мир макроскопический. Один из примеров привел Шрёдингер. Он заметил, что, подобно тому как магнитный момент в рамках квантовой механики может принимать два различных значения, так и обычный кот при расширении последней до масштаба комнаты может находиться в двух состояниях: быть и живым и мертвым одновременно (рис. 6)! Если мы открываем дверь в комнату, мы с равной вероятностью 1/2 можем обнаружить как мертвого, так и живого кота, но пока дверь закрыта, кот одновременно и жив и мертв.

Рис. 6. В мысленном эксперименте Шрёдингер представил себе кота, запертого в герметичной коробке. Устройство, принцип действия которого основан на случайном распаде радиоактивного атома, может разбить колбочку с ядом. По истечении заданного времени вероятность распада атома составляет 1/2. До тех пор пока наблюдатель не откроет коробку, квантовая механика утверждает, что атом одновременно и распался и не распался, следовательно, и кот теоретически и жив и мертв

В 2015 году коту Шрёдингера исполнилось 80 лет! Тем не менее, старея, он становится все более живым. Совсем недавно благодаря усилиям ученых он материализовался из области абстрактных рассуждений и стал реальностью. Конечно, это не настоящий кот, а крошечный объект, который только в шутку называют «котом Шрёдингера». Под этим названием сегодня подразумевают любой относительно макроскопический объект, приведенный в состояние квантовой суперпозиции. Этот котенок (представляющий собой лишь несколько атомов) косвенно стал одним из лауреатов Нобелевской премии по физике, присужденной в 2012 году Сержу Арошу и Дэвиду Уайнленду.

«Это же абсурдно! — может решить читатель. — На самом деле кот либо жив, либо мертв и до открытия двери, неважно, знаем ли мы его состояние». Такое понимание рассматриваемой ситуации базируется на иной, некогда существовавшей интерпретации квантовой механики, основанной на понятии скрытого параметра. Согласно этой концепции, описание мира является детерминистичным, однако некоторые параметры, необходимые для его реализации, оказываются нам недоступными. Современная наука опровергает эту концепцию. Но все же индетерминизм квантовой физики порождает парадоксы, которые интуитивно сложно принять.

Опишем один из них.

Парадокс Эйнштейна-Подольского-Розена (ЭПР-парадокс)

В 1935 году Эйнштейн и его коллеги Борис Подольский и Натан Розен предложили парадокс, который впоследствии стал темой для многих научных работ (некоторые публикуются и в наши дни). Они рассмотрели ситуацию, которую сегодня называют квантовой «запутанностью» (по-английски — entanglement). Здесь задействован уже не один объект, как в парадоксе Шрёдингера, а два. Например, возьмем кота и собаку, хотя оригинальная формулировка парадокса их и не предполагала. Предположим, что одно из животных мертво (какое — неизвестно), а другое живо. Состояние, в котором жив кот, а собака мертва, обозначим \(\left|+- \right>\), а состояние, в котором кот мертв, а собака жива, запишем как \(\left|+- \right>\). В случае если эти два состояния смешаны, говорят, что они запутаны. Запутанное состояние представлено обозначением \((\left|+- \right>+\left|-+ \right>)/\sqrt{2}\). Пока кот и собака находятся в двух отдельных закрытых камерах (звуконепроницаемых и т. п.), неясно, кто из них жив, а кто мертв. Но если мы откроем камеру с котом и обнаружим его мертвым, то узнаем, что собака жива, а если мы обнаружим живого кота, будем знать, что мертва собака: оба наблюдения коррелируют. Отметим, что эта корреляция сохраняется при нахождении животных в двух камерах, расположенных и на расстоянии 1000 км друг от друга. Чтобы узнать, жива ли собака, находящаяся за 1000 км, достаточно открыть камеру с котом. Таким образом, мы получаем информацию мгновенно, хотя никакой сигнал не может распространяться быстрее скорости света! Можно даже подумать, что открытие камеры с котом, которого мы обнаружим живым, мгновенно на расстоянии вызовет смерть собаки, которая до сих пор была только «полумертвой». Конечно, невозможно предугадать исход открытия камеры, потому что мы найдем кота живым или мертвым с одной и той же вероятностью 1/2, равно как и собаку; однако мы понимаем, что Эйнштейн, Подольский и Розен были озадачены. В конце статьи они высказали мнение о необходимости разработки новой квантовой механики. Она могла бы быть основана на предположении о существовании скрытых параметров, т. е. параметров, недоступных для экспериментальной верификации и не входящих в теории Шрёдингера и Гейзенберга.

Неравенства Белла и опыты Аспе

ЭПР-парадокс оспаривали многие исследователи, в том числе и Бор. Другие выдающиеся ученые, в том числе Луи де Бройль и Дэвид Бом, подобно Эйнштейну предпочли бы восстановить детерминизм. Дискуссия длилась долго и носила философский оттенок. В 1964 году Джон Белл смог сделать ее более конкретной и показал, что детерминистическая физика, даже со скрытым детерминизмом, должна включать в себя некоторые доступные измерению неравенства, которые противоречат обычной форме квантовой механики.

Неравенства Белла были проверены Аленом Аспе и его сотрудниками в Париже в 1982 году. Они воспроизвели ситуацию, аналогичную описанной нами чуть раньше. Очевидно, ученые использовали не кота и собаку, поскольку квантовая механика неприменима к макроскопическим объектам, а фотоны, поляризация которых (т. е. направление колебаний электрического поля) может иметь два взаимно ортогональных направления, подобно тому как кошка и собака могут находиться в двух равновероятных состояниях (живом и мертвом). Исследователи намеревались обнаружить корреляцию между поляризациями фотонов. И это лишь одна из многочисленных трудностей эксперимента. Другая сложность была связана с тем, что фотоны двигаются с огромной скоростью, а за время их перемещения следует успеть сделать очень многое. В конечном итоге опыты Аспе привели к выводу, что неравенства Белла не могут быть проверены на достоверность. Значит, квантовая механика, изложенная в учебниках, является правильной и не может быть заменена или дополнена теорией скрытых параметров. Опыт Аспе превратил мысленный эксперимент Эйнштейна, Подольского и Розена в эксперимент реальный.

Статья представляет собой главу из книги «Физика повседневности», выпущенной издательством «Альпина нон-фикшн» в 2020 году.