Джордж Габриель Стокс — классик математической физики ХIХ века

Роберт Щербаков,
доктор педагогических наук (Таллин, Эстония)
«Природа» №1, 2020

Дж. Г. Стокс (1819–1903) — английский математик, механик и физик ирландского происхождения — внес большой вклад в физику: в теоретическую механику, гидродинамику, теорию упругости, теорию колебаний, оптику и математическую физику, а также в математический анализ. Он был членом Лондонского королевского общества, его секретарем и президентом, содействовал развитию точных наук.

Дж. Г. Стокс, 1860-е годы. Библиотека Б. Дибнера по истории науки и техники Смитсоновского института (США)

В Англии XIX в. наряду с математическими дисциплинами получили развитие и физические. Из традиционной натуральной философии (как в то время называлось естествознание) выделилась самостоятельная наука — физика — со своими собственными подходами и методами, с первыми физическими лабораториями и институтами.

Как и многие его соотечественники, Дж. Г. Стокс бережно сохранял и развивал традиции Кембриджа — ведущего естественно-научного научного центра 19-го столетия, суть которых состояла в том, чтобы для решения проблем теоретической механики и оптики использовать в первую очередь математические методы и лишь в редких случаях применять в своих исследованиях эксперимент.

Становление Стокса как ученого

Джордж, младший сын из шести детей протестантского священника-евангелиста Габриэля Стокса, родился 13 августа 1819 г. в Ирландии, в дер. Скрин. Воспитание в семье было религиозным, трое из его старших братьев позднее стали священниками. Да и сам он, посвятив себя науке, сохранил на всю жизнь религиозные взгляды на мир.

В 1835 г. 16-летний Джордж переехал в Англию, где поступил в Бристоле в колледж. Двухлетнее обучение стало важным моментом в развитии его математических способностей и помогло подготовиться для учебы в Кембридже. В 1841 г. Стокс получил университетское образование. В Кембридже он начал и преподавание, а в 1849 г. получил Лукасовскую кафедру математики (самую престижную в мире академическую должность Лукасовского профессора математики он занимал рекордные 54 года), которую в свое время возглавлял И. Ньютон.

Главное здание Кембриджского университета, в котором работал Стокс

За 66 лет научной деятельности Стокс охватил практически все стороны физики своего века, начиная с классических работ по механике и оптике и заканчивая изучением гравитационного поля Земли, гипотетического эфира и применением спектрального анализа. Вне круга его интересов остался лишь электромагнетизм. Ученый внес вклад в теоретическую механику и математическую физику. В этих областях науки Стокс преуспел благодаря удачному и весьма искусному владению математическими методами.

Как подчеркивал Ф. Клейн, свое бесперебойное и блистательное восхождение математическая физика в Англии начала лишь тогда, когда... среди молодых талантов в Кембридже на первый план выдвинулись Стокс и Вильям Томсон... <...> Стокс с 1837 г. и до самой смерти, т.е. в течение 66 лет, жил в Кембридже и вел в нем — сначала в качестве исследователя, а затем в качестве педагога и администратора — свою широкую, непрерывную и, благодаря личной доброте, очень благотворную деятельность [1, с. 259].

Применяя математику, Стокс ставил и эксперименты, которые вначале проводил в комнатах Пемброк-колледжа Кембриджского университета. И только растущая со временем потребность в проведении более точных и объемных измерений побудила ученых Англии создать в 1871–1872 гг. физические лаборатории: Оксфордскую и (усилиями Дж. К. Максвелла) Кавендишскую при Кембриджском университете. Для 52-летнего Стокса это было уже, к сожалению, поздновато.

По словам А. Г. Столетова, посетившего лабораторию Дж. К. Максвелла в момент ее открытия, тогда изучение физики долго сливалось с математическими курсами, и существование особой кафедры для Physics так же ново, как и сам термин... До 1871 г. в Кембридже преподавались только оптика как часть математики и некоторые главы из теплоты как часть химии; обширная наука об электричестве и магнетизме не преподавалась вовсе [2, с. 342].

Возможно, этим и объяснялся выбор английскими учеными той эпохи (в том числе и Стоксом) таких направлений научной деятельности, как математика, теоретическая механика, оптика и гипотетический эфир. Лишь время от времени Стокс для тщательной проверки уже проведенных им теоретических выкладок применял простейшие по нынешним меркам опытные исследования.

Механика и гидродинамика в работах Стокса

Дж. Г. Стокс — вместе с Дж. Грином, У. Томсоном (лордом Кельвином), У. Дж. М. Ренкином, О. Рейнольдсом, Дж. У. Стреттом (лордом Рэлеем) и др. — успешно развивал математические методы и внес посильный вклад в развитие классической математической физики, применяя математику к задачам физики и техники своего времени. Благодаря тому поколению ученых методы математической физики получили развитие для решения целого ряда задач по теплопроводности, диффузии, теории упругости и устойчивости движения, колебательным и волновым процессам, оптике, теории потенциала и электродинамике. Эти методы остаются актуальными и для современной физики, техники и промышленности.

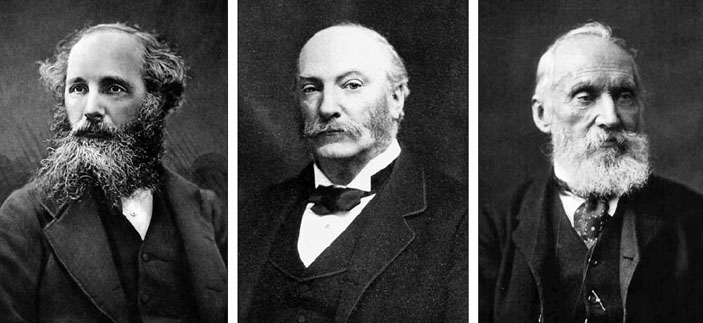
Ближайшие коллеги, ученики и друзья Дж. Г. Стокса, слева направо: Дж. К. Максвелл, Дж. У. Стретт (лорд Рэлей) и У. Томсон (лорд Кельвин)

Как ученый, Стокс от занятий математикой получал эстетическое удовольствие и практическое удовлетворение. Ему удалось указать на полусходящиеся ряды, изучить полностью или ограниченно сходящиеся бесконечные ряды, ввести понятие равномерной сходимости целой последовательности и ряда, а также заняться векторным анализом. Одна из важнейших формул, предложенных им, была названа в честь ученого — это формула Стокса. Она связывает ротор векторного поля¹ с циркуляцией поля по замкнутому контуру, ограничивающему некоторый участок ориентированной поверхности. Формула была получена в 1849 г. также и его другом Томсоном. Сам же Стокс посчитал полезным включить ее в ежегодный экзамен по математике, который проводил с 1849 по 1882 г. В 1910 г. немецкий физик-теоретик А. И. В. Зоммерфельд обобщил выводы Стокса на четырехмерное пространство. Дж. К. Максвелл в работе «О фарадеевских силовых линиях» (1885–1886) показал существенную роль теорем и формул векторного анализа, связанных с именами выдающихся ученых К. Ф. Гаусса, Дж. Грина, М. В. Остроградского, У. Томсона и, разумеется, Дж. Г. Стокса — своего старшего друга.

Вначале ученые полагали, что между механикой жидкости и газов и механикой твердого тела нет ничего общего. Но в 1845 г. Стокс обнаружил общие свойства твердых тел и вязких жидкостей. Рассматривая пластичность твердого тела, он пришел к выводу, что с повышением пластичности вещества уменьшается его упругость и твердое тело переходит в жидкое состояние. Идеи Стокса оказались ценными, они стимулировали серию последующих научных исследований.

Изучением вязкой жидкости успешно занимались французские ученые Л. М. А. Навье², О. Л. Коши, С. Д. Пуассон и др. Стокс в 1849 г. в статье «О теории внутреннего трения в движущихся жидкостях и о равновесии и движении упругих твердых тел» дополнил теорию Навье, получив дифференциальные уравнения для вязких жидкостей и газов (не связанные с представлением о молекулах). Они известны сегодня как уравнения Навье — Стокса. В честь ученого единица кинематической вязкости³, входящая в систему СГС, позднее была названа стоксом (русское обозначение: Ст; международное St). В Международной системе единиц СИ единицей измерения вязкости служит м²/с: 1 Ст = 1 см²/с = 10⁻⁴ м²/с.

Стоксом же была построена теория ламинарного пограничного слоя. Именно он установил факт перехода ламинарного обтекания тела в турбулентное — вначале для водопроводных труб и тел, обтекаемых потоком жидкости (исследование проводилось с целью изучить влияние отрыва пограничного слоя на величину сопротивления). Со временем теория турбулентности получила существенное развитие, вызванное возросшими скоростями судов, самолетов, работой турбин и паровых машин.

По определению историка науки И. Б. Погребысского, внимание к физической стороне дела, учет экспериментальных результатов, ясная кинематическая картина движения и исчерпывающая формулировка исходного динамического принципа — все это в сочетании с несколькими удачными применениями теории сделало работу Стокса основным отправным пунктом для дальнейших работ по теории вязкой жидкости [3, с. 127].

Пренебрегая нерегулярной составляющей скорости жидкости, зависящей от расстояний между молекулами и взаимодействий между ними, Стокс оперировал лишь средней регулярной скоростью жидкости в окрестности жидкой частицы. Гипотеза, позволившая ему вывести уравнение движения вязкой жидкости, была основана на линейной зависимости шести компонент напряжения от шести компонент скоростей деформации жидкой частицы.

Рассматривая жидкость как сплошную среду, Стокс обратился к понятию «внутреннее трение». Опираясь на свои расчеты, он внес поправки в проведенный Ньютоном анализ задачи о вращении вязкой жидкости в цилиндре. Как показал Стокс, ошибка Ньютона была в том, что вместо моментов сил трения, действующих на внешнюю и внутреннюю поверхности каждого из мысленно выделяемых в жидкости слоев, он рассматривал сами силы. У Ньютона оказывалось, что время одного оборота жидкой частицы зависит от радиуса цилиндрического слоя линейно, а из результатов Стокса следовало, что данное время пропорционально квадрату радиуса. В итоге ему удалось теоретически объяснить и формулу Гагена — Пуазейля для расхода вязкой несжимаемой жидкости при стационарном течении в цилиндрической трубе. В конечном счете сам Стокс получил дифференциальные уравнения, описывающие закон изменения скорости со временем.

В 1851 г. ученый вывел формулу для силы сопротивления F, действующей на малый твердый шар при его медленном равномерном движении в неограниченной вязкой жидкости. Формула Стокса имеет вид: F =  6πRηu, где R и u — радиус и скорость шара, а η — динамический коэффициент вязкости жидкости. Закон оказывается верным и при очень малых радиусах, и позднее А. Эйнштейн применил его для измерения радиуса молекулы сахара.

Закон Стокса широко применялся в новых исследованиях. Напомню о расчетах броуновского движения А. Эйнштейном, об определении зарядов иона Дж. Дж. Томсоном и электрона Р. Милликеном. Анализ учеными опытов Милликена и их собственные опыты показали, что ошибочно взятая Милликеном величина вязкости воздуха в формуле Стокса привела его к не вполне точному определению элементарного заряда. Однако в результате новых проверок была лишь подтверждена верность закона Стокса.

В работе «О теории внутреннего трения в движущихся жидкостях...» (1845) Стокс показал [4, с. 116], что свойство тел совершать изохронные колебания вызвано тем, что при малых деформациях напряжения, возникающие в теле, имеют характер линейных функций деформаций. Исследовал он и прогиб мостов. Узнав о разрушении железнодорожного моста в Уэльсе, он установил, что виной тому была хрупкость чугуна при деформации. Исследования Стокса по динамическому прогибу мостов близки к прикладным работам, к технике. При этом он, как обычно, отказался от представлений о молекулярной структуре тел и вновь посчитал, что исходные положения следует черпать из оптики. Занимаясь теорией упругости и рассматривая упругие и пластические тела, ученый полагал, что в природе упругость и пластичность неотделимы друг от друга и, более того, между ними не существует резкого перехода.

Стокс занимался также изучением поглощения звука в жидкости. Но проведенный им анализ был неполным, ибо в качестве диссипативного (рассеивающего) механизма он рассматривал вязкость, но не учитывал теплопроводность. Однако этого и нельзя было сделать, пока Ю. Р. фон Майер, Дж. П. Джоуль и Г. Л. Ф. фон Гельмгольц не открыли закон сохранения энергии, который вначале был принят научным сообществом с недоверием.

Уже на первых порах своей научной деятельности Стокс зарекомендовал себя крупным механиком и гидродинамиком. Подобно Ф. Э. Нейману, Ж. А. Пуанкаре, П. М. М. Дюгему, Т. Леви-Чивите, М. В. Остроградскому и П. Л. Чебышеву, он внес вклад в разработку теоретических основ механики. При этом теория упругости разрабатывалась им с позиций механики, известных на тот момент представлений физиков и поставленных экспериментов. К 60-м годам ХIХ в. молодой Джордж Стокс стал уже известен в научной среде Кембриджа как состоявшийся исследователь в теоретической механике, математической физике и гидравлике, как специалист в оптике и одновременно как терпеливый и весьма благожелательный воспитатель новых поколений ученых.

Исследования Стокса по волновой теории света

Как раз в те годы в науке, наряду с механизацией физики и основ теории упругости, создавалась волновая теория света, а также появилась гипотеза О. Ж. Френеля о квазитвердом эфире, частично увлекаемом движущимися телами; возникли и математические теории эфира. Во всех этих событиях важная роль принадлежала и Стоксу. В частности, крупный вклад был им внесен в развитие оптики. Всю жизнь ученый оставался сторонником волновой теории света и использовал соответствующий математический аппарат, а опыты проводил практически в тех же условиях, что и Ньютон.

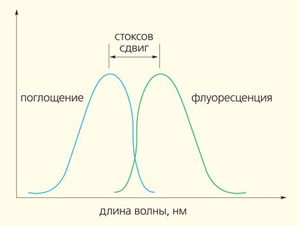
Схематическое представление стоксова сдвига, выражающего разницу длин волн максимумов спектров поглощения и фотолюминесценции. Сдвиг означает, что длина волны люминесценции больше, чем длина волны возбуждающего света, а частота люминесценции, соответственно, меньше частоты возбуждающего излучения

Стокс (как и большинство его современников) исследовал оптические феномены: аберрацию света⁴, кольца Ньютона, интерференцию и поляризацию света, а также прохождение волны через среды и спектры. Его вклад в волновую теорию оказался настолько весомым, что позднее его ученик Стретт в своем труде «Волновая теория света» поставил Дж. Г. Стокса на второе место (после О. Ж. Френеля) по числу ссылок на его работы [4, с. 206].

В 1852 г. Стокс удачно предложил использовать величины, описывающие вектор поляризации электромагнитных волн. Введенные им параметры предлагали формулы, которые представляли собой столбец-вектор и имели размерность интенсивности света. Подробные параметры стали альтернативой описанию некогерентного или частично поляризованного излучения в терминах полной интенсивности, степени поляризации и формы эллипса поляризации.

Занимался Стокс и люминесценцией, обнаруженной им при наблюдениях на плавиковом шпате (флюорите). В том же 1852 г. Стокс пришел к выводу (обобщенному позже Э. К. Й. фон Ломмелем и С. И. Вавиловым), что лучи, испускаемые флюоритом, меньше преломляются, чем поглощенные, а длина волны самой фотолюминесценции больше длины волны возбуждающего света. Это правило, названное в честь Стокса, как показало время, указывает на квантовый характер фотолюминесценции.

В 1879 г. Ломмель обнаружил, что в некоторых частях спектра частоты излучения оказываются больше частот возбуждающего света. Такие части спектра, противоречащие правилу Стокса, назвали антистоксовскими. Вслед за методом скрещенных призм, предложенным Ньютоном, Стокс ввел наблюдения люминесценции посредством метода скрещенных светофильтров, предложив способ обнаружения и изучения близкой ультрафиолетовой области при помощи люминесценции.

В 1905 г. Эйнштейн в статье «Об одной эвристической точке зрения, касающейся возникновения и превращения света» заметил [5, с. 103], что если свет состоит из квантов, то отклонения от правила Стокса возможны по двум причинам: во-первых, когда число квантов в единице объема велико (квант возбуждаемого света может получить энергию от многих возбуждаемых квантов); во-вторых, если энергия испущенного кванта при люминесценции больше энергии кванта возбуждающего.

Во времена Стокса работы по люминесценции носили случайный характер. Основательному же ее исследованию Вавилов посвятил 30 лет своей жизни. Именно он определил границы действия правила Стокса, связал второе начало термодинамики с законом Стокса, сформулировал абсолютный выход люминесценции, создал классификацию ее типов и связал ее с природой элементарных излучателей. В 1950 г. ученый подвел итоги в труде «Микроструктура света». Чуть позже Вавилов отметил, что, несмотря на открытие некоторых общих закономерностей, к числу которых прежде всего относится правило Стокса, люминесценция оставалась уединенным островком физики... <...> И только на основе учения о квантах в 1905 г. Эйнштейн объяснил смысл правила Стокса, а в 1913 г. квантовая теория строения атомов Бора сделала понятными основные черты всей области люминесценции, всех ее разделов [6, с. 335, 338].

Какую из теорий эфира считать верной?

На долгую жизнь Стокса пришлась эпоха создания нескольких теорий эфира — своего рода всепроникающей среды, чьи колебания проявляют себя как электромагнитные волны, в том числе как видимый свет. Свое толкование эфира предлагали О. Ж. Френель, О. Л. Коши, У. Томсон, Х. А. Лоренц, Ж. А. Пуанкаре, М. К. Э. Л. Планк и др. Не прошел мимо этой проблемы и Стокс.

Эфир в представлениях разных ученых отличался степенью однородности, сжимаемости и т.д., а также тем, насколько он увлекался Землей при движении по орбите. В зависимости от своего понимания особенностей эфира ученые по-разному толковали и уравнения Максвелла, к которым, как известно, Стокс с Томсоном относились сдержанно. Отказ от эфира последовал лишь с созданием теории относительности Эйнштейном.

В частности, Френель выдвинул гипотезу, согласно которой эфир несжимаем, но допускает поперечные сдвиги, что было трудно связать с его проницаемостью по отношению к веществу. Стокс объяснил это затруднение тем, что, подобно смоле, эфир при быстрых деформациях ведет себя как твердое тело, а при движении планет пластичен. В 1839 г. Коши улучшил эту модель, создав теорию сжимающегося эфира, позднее доработанную Томсоном.

Создавая в 1845 г. теорию аберрации — изменения направления распространения света при переходе из одной системы отсчета в другую, — Стокс исходил из предположения, что Земля при движении увлекает окружающий ее эфир. В итоге скорость эфира на самой поверхности Земли равна скорости планеты. Ученый допускал, что движение увлекаемого эфира носит характер безвихревого как в пространстве, окружающем планету, так и вплоть до областей, где он пребывает в покое. По Стоксу, эфир одновременно и твердый, и мягкий, но обычно ведет себя как жидкая среда.

Гипотетическая схема (слева) обдува поверхности Земли потоками галактического эфирного ветра (1 — зона повышенного давления эфира; 2 — зона пониженного давления эфира; 3 — зона захвата влаги из океана; 4 — присоединенный тороидальный вихрь эфира, захватывающий зимой воздух атмосферы) и карикатура на нее, свидетельствующая о безуспешности поиска учеными эфира в природе

Стокс предложил следующее объяснение эффекта аберрации. На некотором расстоянии от поверхности нашей планеты должна появляться разность скоростей между увлекаемой частью эфира и эфиром в целом. Такая разность будет обуславливать поворот фронта световой волны, попадающей в оптический прибор. Это и приводит к аберрации. Свое объяснение Стокс дополнил расчетами, доказывавшими, что движение эфира получается невихревым в виде потенциала скоростей. Позднее Планк положительно отнесся к теории Стокса и попытался спасти ее, но безрезультатно.

Впоследствии Стокс уточнил: степень увлечения эфира должна зависеть не только от разности его плотностей. Можно ожидать, что эфир будет уплотняться при вхождении в вещество и разреживаться, выходя из него и притягиваясь к частицам вещества. Учение об упругом эфире сохранялось в научной среде весьма долгое время. Фактически все выдающиеся физики того времени, в том числе и Стокс, занимались разгадкой его свойств и сущности в целом.

В 1846 г. Стокс написал: Вряд ли мы поверим без весьма серьезных оснований, что эфир совершенно беспрепятственно движется сквозь твердую массу Земли. Несмотря на это, было бы очень полезно провести такой решающий опыт, который позволил бы проверить, какую из теорий считать верной [7, с. 235]. В 1881 г. А. А. Майкельсону показалось, что в опытах удалось установить то, что эфирный ветер увлекается Землей, как и предполагал Дж. Г. Стокс. Впрочем, отказ от эфира был уже близок.

Об этом догадывался как сам Стокс, так и его коллеги, придерживавшиеся концепции эфира, тем более что ни один из них так и не смог создать его полноценную теорию. По замечанию И. Физо, среди предложенных на 1851 г. гипотез эфира есть более или менее вероятные, но ни одна не может считаться доказанной [6, с. 214]. И хотя десятилетие спустя Стокс продолжал обсуждать сильные и слабые стороны очередной гипотезы, сам он вряд ли надеялся на ближайший успех.

Уже после смерти Стокса, в 1905 г., Эйнштейн выдвинул принцип относительности и постоянство скорости света. По его выводам, эти предпосылки достаточны для того, чтобы... построить простую, свободную от противоречий электродинамику движущихся тел. Введение «светоносного эфира» окажется при этом излишним... [7, с. 8]. С этого момента многочисленные теории эфира, как и теория Стокса, стали терять свою ценность.

Оценка исследований ученого

Изучение спектра света, начатое И. Ньютоном, было продолжено исследованиями У. Х. Волластона, Й. Фраунгофера, Дж. Ф. У. Гершеля, Ч. Уитстона и Дж. Г. Стокса. Приобрели известность и труды Г. Р. Кирхгофа по изучению излучения тел. Его опытные работы с химиком Р. В. Бунзеном привели к открытию эффекта обращения линий спектра, к объяснению фраунгоферовых линий и к созданию важного для физики, химии и астрономии метода спектрального анализа.

О вкладе Дж. Г. Стокса в эту область физики написал его современник У. Томсон. Он напомнил, что принципы солнечной и звездной химии Стокса излагались последние восемь или девять лет на публичной лекции... Их применение в исследованиях Бунзена и Кирхгофа (открывших независимо от Стокса эту теорию)... показало, что на Солнце имеются железо, магний и некоторые другие известные металлы... <...> Уже много лет назад Стокс в разговоре высказал идею, что, по-видимому, по темным линиям солнечного спектра можно было бы заключить о химических свойствах солнечной атмосферы [8, с. 114].

Вместе с тем Стокс решал и задачу об определении внешнего гравитационного поля Земли по ее уровневой поверхности, массе и угловой скорости вращения около оси. Он доказал разрешимость этой задачи и дал приближенное решение для сжатого сфероида с относительной ошибкой порядка квадрата его сжатия как первой краевой задачи теории потенциала. Вполне точное решение проблемы Стокса для эллипсоида было дано итальянцем П. Пиццетти и М. С. Молоденским⁵ в 1945 г.

В Кембридже применение математических методов в естественных и технических науках поощрялось, широко использовал их также и Стокс. Это проявлялось в том, что, как отметил Вейль, все интегральные теоремы векторного и тензорного анализа являются частными случаями общей теоремы Стокса для дифференциальной формы порядка r на r-мерном (ориентируемом) многообразии, вложенном в пространство с координатами х_i [9, с. 192].

Действительно, Стокс внес важный вклад в развитие математики. Его имя носит одна из главных формул векторного анализа — формула Стокса, которая связывает ротор векторного поля с циркуляцией этого поля по замкнутому контуру, ограниченному некоторым участком ориентированной поверхности. Формула была получена в 1849 г. У. Томсоном; Дж. Г. Стокс же со своей стороны указал на полусходящиеся ряды, исследовал полностью или ограниченно сходящиеся бесконечные ряды.

В 1848 г. одновременно с немецким математиком Ф. Л. фон Зейделем Дж. Г. Стокс ввел в научный обиход понятие равномерной сходимости последовательности и ряда. При этом его интересовала не только чистая математика, но и ее применение в разных разделах физических (механика и оптика), астрономических и технических наук. В историю науки вошли: явление Стокса в асимптотическом анализе, параметры и вектор Стокса в гидродинамике, его теоремы в дифференциальной геометрии, линия Стокса, связи и сдвиг в оптике, уравнение Навье — Стокса, дрейф Стокса, функции тока и волны Стокса, пограничный слой Стокса в гидродинамике.

Не умаляли заслуг Стокса в науке и поправки к его работам. Так, П. Н. Лебедев с учеником Н. П. Неклепаевым⁶ сомневались в точности коэффициентов в формулах для акустических волн Стокса и Кирхгофа [10, с. 349]. У. Г. Брэгг отметил, что импульсная теория Стокса (ускоренный электрон вызывает импульсы в эфире) не объясняет взаимозаменяемость Х-лучей и электронов. Р. Э. Милликен подчеркивал, что закон движения капли совпадает с законом Стокса лишь в случае непрерывной среды. Были и другие замечания по работам ученого.

Стокс продолжал свои исследования и в последние годы жизни. В частности, он не мог пройти мимо открытия Рентгена. В 1898 г. в статье «О природе рентгеновских лучей» он попытался теоретически разобраться с краткими импульсами электромагнитного характера, которые возникают на антикатоде в результате торможения падающих на него частиц катодного пучка. Как и немецкий физик И. Э. Вихерт, Дж. Г. Стокс пришел к выводу о том, что из самого способа возникновения рентгеновских лучей следует, что они представляют собой световое излучение с очень короткой длиной волны.

Стокс как организатор науки и педагог

При жизни Стокса окружали выдающиеся ученые Англии, начиная с М. Фарадея и заканчивая Э. Резерфордом и другими, еще ожидавшими своего звездного часа.

До конца дней Стокс был в курсе научных событий, критически (хотя и не всегда верно) оценивая их. Так, он сдержанно, как и У. Томсон, отнесся к «Трактату» Дж. К. Максвелла, зато сразу признал открытие В. Рентгеном Х-лучей, о чем поспешил сообщить ему в письме.

Стокс с соратниками внесли немалый вклад в развитие точных и прикладных наук, в уточнение методов разгадки физических явлений, в разграничение научного знания от натурфилософского, научной деятельности от эмпирической. Благодаря ему и таким, как он, качество университетского образования было приведено в соответствие с потребностями будущих исследователей. Стокс десятилетиями занимался чтением лекций. Его слушал и Максвелл, ставший со временем ближайшим другом Стокса.

По воспоминаниям Стретта, лекции и опыты Стокса произвели на него впечатление и научили его многому полезному в преподавании. Когда слушатели курса Стокса обращались к нему за разъяснением непонятых ими оптических явлений, он, как правило, был отзывчив и любезен.

О традициях английского образования второй половины XIX — начала XX в. писал П. Л. Капица, знакомый с традициями Кавендиша. Он отмечал, что, во-первых, объясняя студенту, можешь быть уверен, что сам понимаешь вопрос. Во-вторых, когда ищешь форму ясного... изложения... приходят новые идеи. В-третьих, вопросы студентов стимулируют мысль и заставляют с новой точки зрения взглянуть на явление, к которому подходим всегда стандартно, и это тоже помогает творчески мыслить [11, с. 261]. Так в свое время поступал и Стокс.

Из своего сборника Стокс рекомендовал студентам решить ту или иную задачу, связанную с проблемой физики или математики. В одной из них предлагалось доказать, что интеграл, взятый по контуру, связан с величиной проходящего через него потока. Сегодня бы сказали, что для этого нужно доказать теорему Стокса, хотя сам ученый никогда не публиковал ее доказательства. В 1854 г. при сдаче трайпоса (публичного экзамена на степень бакалавра с отличием в Кембриджском университете) аспирант Максвелл у Стокса решил задачу на распределение молекул по скоростям в газе.

С 1887 по 1892 г. Стокс был одним из членов парламента от Кембриджского университета. Несмотря на столь ответственную должность, а возможно, из-за его рационального склада ума и уравновешенного характера, он редко позволял себе выступать в палате общин, оставаясь при этом внимательным слушателем.

Воспитанный в семье с прочными религиозными устоями, Стокс и в жизни придерживался консервативных ценностей и убеждений. В 1886 г. он стал президентом Института Виктории⁷, основанного для охраны христианских принципов от вызовов новой науки, особенно дарвиновской теории эволюции, чьим критиком был и Стокс. Был он также вице-президентом британского и иностранных Библейских обществ, поддерживая их миссионерскую работу.

Парадный портрет президента Королевского общества сэра Дж. Г. Стокса кисти Г. ван Геркомера (Лондонское королевское общество)

В 1851 г. Стокс стал членом Лондонского королевского общества, затем его секретарем, а в 1885–1890 гг. — президентом. В 1849–1903 гг. он был Лукасовским профессором Кембриджского университета. За исследования света в 1852 г. получил медаль Румфорда от Королевского общества, а в 1893 г. — медаль Копли. Хлопотами Стретта ему в 1889 г. был присвоен титул баронета, от Французской академии вручена медаль Араго, стал он и членом российской Императорской военно-медицинской академии.

Оценивая стиль Стокса, Дж. Лармор, написавший о нем книгу, отметил: Стокс возводил осторожность в крайность... <...> Опубликованные исследования Стокса характеризуются... преобладающим тоном, точностью и строгой оформленностью определений, относящихся к свойствам и закономерностям вещества, взятого в массе, чем исключается даже всякая нужда в использовании понятия молекулы [12, с. 329].

По существу творчество Стокса стало органичной составляющей научной культуры того времени. Многочисленные ссылки ученых XIX–XX вв. на работы Стокса, стремление уточнить и развить их в своих исследованиях свидетельствовали о том, что его усилия не пропали даром и служили благодатным материалом, который стимулировал дальнейшие успехи науки нашего времени.

Некоторые члены Лондонского королевского общества. Гравюра на дереве, 1885 г. (Wellcome Library, № 545240i). Сэр Дж. Г. Стокс, президент Королевского общества, сидит в первом ряду слева

Наследие классика науки

Открытия Стокса — в первую очередь, закон Стокса, теорема Стокса, стоксов сдвиг, уравнение Стокса и его параметры — вошли в науку и технику, активизируя деятельность зарубежных и российских ученых по их развитию. Достаточно напомнить, что Н. Бор, уточняя теорию Рэлея, в 1909 г. обращался и к методам Стокса.

Медаль, выпущенная к 100-летию со дня рождения Стокса

При жизни Дж. Г. Стокса продолжали свои научные исследования М. Фарадей, Дж. К. Максвелл, Д. П. Джоуль и Г. Р. Герц (они уйдут из жизни в 1867, 1879, 1889 и 1894 гг. соответственно), У. Томсон, У. Рамзай, Дж. У. Стретт и другие его коллеги. В общении и спорах с ними он обогащался и вдохновлялся новыми идеями, получая импульс к дальнейшим открытиям в своей творческой деятельности.

Его открытия продолжали будоражить воображение ученых даже тогда, когда Стокса не стало, приводя их к новым свершениям, но уже с позиций квантовой теории и теории относительности. В развитие представлений Дж. Г. Стокса внесли вклад Х. А. Лоренц, М. К. Э. Л. Планк, А. Эйнштейн, Н. Бор, А. А. Майкельсон, Р. Э. Милликен, А. Х. Комптон, А. Ф. Иоффе, Я. И. Френкель, С. И. Вавилов и другие ученые ХХ в.

Книг о своих исследованиях Стокс не писал, но по числу опубликованных статей был одним из самых плодовитых авторов Королевского общества, Британской ассоциации содействия науке (в 1869 г. он был ее президентом), Института Виктории и других научных организаций. Итоги его деятельности, отраженные им в статьях, становились предметом переписки с коллегами из разных стран.

Работы Стокса были собраны и изданы в пяти томах «Mathematical and Physical Papers» (1880–1905), при этом первые три тома отредактировал он сам. Последние два тома вышли в свет уже после смерти ученого в 1905 г. с некрологом, написанном Стреттом.

В 1907 г. в двух томах была опубликована краткая биография Стокса и его научная переписка, подготовленная Дж. Лармором. Был также создан фонд Стокса для поощрения молодых талантов (мемориальный курс для чтения лекций английскими и зарубежными учеными).

Обложки трех томов статей Стокса по физике и математике, переизданных Кембриджским университетом в конце XX в.

Умер Джордж Габриель Стокс в Кембридже 1 февраля 1903 г. в возрасте 83 лет. Похоронен на кладбище Милл Роуд. Увы, но могила его не сохранилась, в отличие от могил его жены и двух детей. В честь ученого названы: единица измерения вязкости в системе СГС, кратеры на Луне и Марсе, минерал стокезит.

Литература
1. Клейн Ф. Лекции о развитии математики в XIX столетии. Т. 1. М., 1989.
2. Столетов А. Г. Собрание сочинений. Т. 1. М.; Л., 1939.
3. Погребысский И. Б. От Лагранжа к Эйнштейну. М., 1996.
4. Стрэтт Дж. В. (лорд Рэлей). Волновая теория света. М., 2015.
5. Эйнштейн А. Собрание научных трудов. Т. III. М., 1966.
6. Творцы физической оптики: Сборник статей. М., 1973.
7. Эйнштейн А. Собрание научных трудов. Т. I. М., 1965.
8. Кирхгоф Г. Избранные труды. М., 1988.
9. Вейль Г. Математическое мышление. М., 1989.
10. Лебедев П. Н. Собрание сочинений. М., 1963.
11. Капица П. Л. Эксперимент. Теория. Практика. М., 1981.
12. Тимошенко С. П. История науки о сопротивлении материалов. М., 1957.

¹ Ротор векторного поля показывает, насколько и в каком направлении закручено поле в каждой точке.

² Луи Мари Анри Навье (1785–1836) — французский математик и механик, один из основоположников теории упругости, с 1824 г. член Парижской академии наук.

³ Кинематическая вязкость — отношение динамической вязкости плотности среды к жидкости, дает понятие о ее вязкости под действием силы тяжести (измеряется вискозиметром по времени вытекания из калиброванной емкости).

⁴ Аберрация света — изменение видимого положения светила в небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли.

⁵ Михаил Сергеевич Молоденский (1909–1991) — советский геофизик, гравиметрист и геодезист. Разработал теорию использования измерений гравитационного поля Земли для целей геодезии. Предложил метод астрономо-гравиметрического нивелирования, новый метод определения.

⁶ Николай Павлович Неклепаев (1886–1942), ученик П. Н. Лебедева, исследовал вместе с ним поглощение акустических волн, преподавал в Московском университете, затем был ассистентом при кафедре физики Саратовского университета.

⁷ Институт Виктории (или Философское общество Великобритании) был основан в 1865 г. как ответ на публикацию книги Ч. Дарвина «О происхождении видов...». Институт Виктории пользовался значительным успехом в конце XIX в., когда Дж. Г. Стокс был его президентом (с 1886 г. до своей смерти). Максимальное число членов — 1246 человек — было в 1897 г., но быстро упало до менее чем трети от этого количества в первые два десятилетия XX в. Дж. К. Максвелл неоднократно приглашался для вступления в институт, но, хотя он и был набожным евангелистом-христианином, он отказался от приглашений из-за узости тематики и консерватизма института.